PHY1160C
Exam #1
September 15, 2000

Name ______________________________

 | Return to Calendar |

This exam is fairly lengthy or long. Pace yourself accordingly. Do not spend too much time on any one problem.

It will be easy to spend too much time on the first two problems. Resist that temptation. Spread your time and efforts over all of the questions.

Possibly useful information:

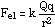
k = 9 x 109 N m2/C2

e = 1.6 x 10 - 19 C
me = 9.11 x 10 - 31 kg

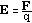
PE = k Q q / r

V = k Q / r


Ceq = C1 + C2 + C3

P = IV = I2R = V2/R

Req = R1 + R2 + R3 + . . .


q = Qf e - t/RC

i = Io e - t/RC
q = Qf [ 1 - e - t/RC ]

i = Io [ 1 - e - t/RC ]

 | Return to Calendar |

1. What is the electric field at the origin (x = 0, y = 0) when charges Q1 = - 10 µC and Q2 = - 30 µC are placed at corners of a square, 10.0 cm (0.10 m) on a side, as shown in the figure below? What is the electric field -- magnitude and direction -- at the origin?

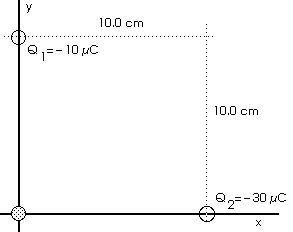
Diagrams always help,

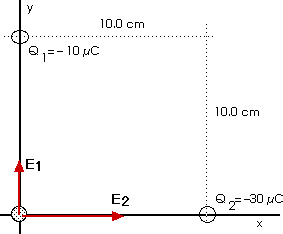
First we will calculate E1, the field due to charge Q1 and find its direction. Then we will calculate E2, the field due to charge Q2 and find its direction. Then we will find the vector sum of these two electric fields for the net field E.

E1 = 9.0 x 10 6 N/C

and this field points upward. That is,

E1x = 0

E1y = + 9.0 x 10 6 N/C

Now for the field due to the other charge, Q2,

E2 = 2.7 x 10 7 N/C

and this field points to the right. That is,

E2x = 2.7 x 10 7 N/C

E2y = 0

The net field is the vector sum of these,

Enet = E1 + E2

which is shorthand notation for

Enet,x = E1x + E2x and Enet,y = E1y + E2y

Enet,x = 0 + 2.7 x 10 7 N/C Enet,y = + 9.0 x 10 6 N/C + 0

Enet,x = + 2.7 x 10 7 N/C Enet,y = + 9.0 x 10 6 N/C

Enet,x = + 27 x 10 6 N/C Enet,y = + 9.0 x 10 6 N/C

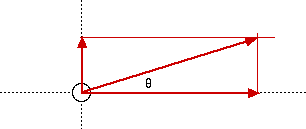
Now we have the components of the field and we can construct the field itself -- that is, we can calculate its magnitude and direction.

E = 28.5 x 10 6 N/C

= 18.4°

That is, the net electric field E is
E = 28.5 x 10 6 N/C at the angle = 18.4o

as shown in the diagram.

 

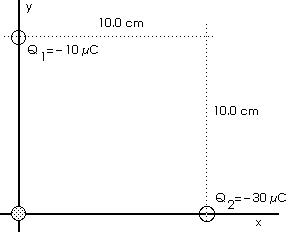
2. What is the electric potential at the origin (x = 0, y = 0) when charges Q1 = - 10 µC and Q2 = - 30 µC are placed at corners of a square, 10.0 cm (0.10 m) on a side, as shown in the figure below. What is the electric potential at the origin?

The electric potential due to a point charge is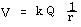

Vtot = Vi = V1 + V2

V1 = k Q1 / r1

V1 = ( 9 x 10 9 ) ( - 10 x 10 - 6 ) / 0.10

V1 = - 9 x 10 5 volts

V2 = k Q2 / r2

V2 = ( 9 x 10 9 ) ( - 30 x 10 - 6 ) / 0.10

V2 = - 2.7 x 10 6 volts = - 27 x 10 5 volts

Vtot = V1 + V2

Vtot = ( - 9 - 27 ) x 10 5 volts

Vtot = - 36 x 10 5 volts

Vtot = - 3.6 x 10 6 volts


3. Three capacitors are connected in the circuit shown below. They have values of C1 = 150 µF, C2 = 250 µF, and C3 = 500 µF. They are connected to a 12-volt battery as shown. Find the charge on each capacitor and the potential energy stored in capacitor C1.


First, we replace the parallel capacitors, C2 and C3, with a single equivalent capacitor which we will call Ceq1:

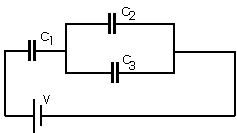
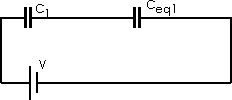
Ceq1 = C2 + C3

Ceq1 = (250 + 500) F

Ceq1 = 750 F 

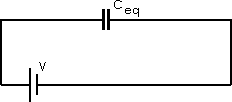
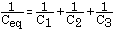
Now we replace these series capacitors, C1 and Ceq1, with a single equivalent capacitor which we will call Ceq:

Ceq = 125 F

C = Q/V ===> Q = C V

Q = ( 125 x 10 - 6 F )( 12 V )

Q = 1.5 x 10 - 3 C

Now, for the total energy supplied by the battery, 

PETot = [1/2] Q V = [1/2] [1.5 x 10 - 3 C] [12 V]

PETot = 9 x 10 - 3 J = 9 mJ

 

Now we return to the individual capacitors,

Q1 = Q = 1.5 x 10 - 3 C

Note that the voltage across capacitor C1 is not 12 V !

V1 = 10.0 V

This means the voltage across the parallel part, C2 and C3, must be

V2 = V3 = 12 V - V1 = 12 V - 10 V

V2 = V3 = 2.0 V

Now, for the potentential energy stored in the capacitors,

PEcap = [1/2] Q V

PE1 = [1/2] Q1 V1

PE1 = [1/2] ( 1.5 x 10 - 3 C )( 10 V ) = 7.5 x 10 &endash; 3 J = 7.5 mJ

PE1 = 7.5 mJ

Now for the other capacitors,

V2 = V3 = 2.0 V

Note that V2 is not 12.0 V !

Q2 = C2 V2 = (250 x 10 - 6 F) (2.0 V) = 5 x 10 - 4 C = Q2

Q2 = 5 x 10 - 4 C = 0.5 x 10 - 3 C

Q2 = 0.5 x 10 - 3 C

PE2 = [1/2] Q2 V2 = [1/2] ( 5 x 10 - 4 C ) (2 V)

PE2 = 5 x 10 - 4 J = 0.5 mJ 

V3 = 2.0 V

Q3 = C3 V3

Q3 = (500 x 10 - 6 F) (2.0 V) = 1 x 10 - 3 C

Q3 = 1 x 10 - 3 C

PE3 = [1/2] Q3 V3 = [1/2] ( 1 x 10 - 3 C ) (2 V)

PE3 = 1 x 10 - 2 J = 1.0 mJ

 Notice that

PETot = 9 mJ = 7.5 mJ + 0.5 mJ + 1.0 mJ = PE1 + PE2 + PE3

and that

Q = Q1 = 1.5 x 10 - 3 C = 0.5 x 10 - 3 C + 1 x 10 - 3 C = Q2 + Q3

4. Find the equivalent resistance in the circuit shown below for R1 = 100 , R2 = 500 , R3 = 1000 , R4 = 400 . If these are connected to a 12-volt battery, what is the power supplied by the battery? Find the current through resistor R1 and the power supplied to R1.

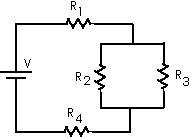
Resistors R2 and R3 are in parallel so we begin by replacing them with an equivalent resistor Req whose value we can calculate from
1/Req = 1/R2 + 1/R3 = 1/(500 ) + 1/(1000 )

1/Req = (0.003) /

Req = [1/0.003] = 333.3

[ Notice that Req < 500 or that Req < Rmin; that is, notice that the equivalent resistance Req is less than the smallest (or smaller) of the resistors in parallel. ]

Now we have R1, this Req, and R4 in series as in the following diagram,

or

The new equivalent resistor Req,2 for this combination of three resistors in series is given by

Req,2 = R1 + Req + R4

Req,2 = 100 + 333 + 400

Req,2 = 833

The current from the battery is given by

I = V / Req,2 = 12 V / 833 = 0.0144 A

This is the current through R1 and R4,

I1 = I4 = 0.0144 A

The power supplied from the battery is

P = I V = (0.0144 A)(12 V) = 0.173 W

Pbat = 0.173 W

Now we work back and find the power absorbed by each of the resistors (well, at least find the power absorbed by resistor R1 since that was asked for in this question). We know the current through R1 and R4 so we can find the voltage across them and then find the power absorbed by them.

V1 = I R1 = (0.0144 A)(100 ) = 1.44 V

P1 = I V1 = (0.0144 A)(1.44 V) = 0.021 W

Only I1 ( = 0.0144 A) and P1 ( = 0.021 W) were asked for in this question. We have found those now. The required solution is complete.

But we might as well continue and find the current and power for all of the resistors -- just for "completness".

V4 = I R4 = (0.0144 A)(400 ) = 5.76 V

P4 = I V4 = (0.0144 A)(5.76V) = 0.0829 W

The voltage across the bank of resistors in parallel -- R2 and R3 -- is the 12 V of the battery minus the voltage across R1 and R4,

V2 = V3 = 12 V - 1.44 V - 5.76 V = 4.80 V

P = I V = (V / R) V = V2/R

P2 = (4.80 V)2 / (500 ) = 0.0461 W

P3 = (4.80 V)2 / (1000 ) = 0.023 W

I2 = V2/R2 = 4.80 V / 500 = 0.0096 A

I3 = V3/R3 = 4.80 V / 1000 = 0.0048 A

As a quick check, see if these absorbed powers equal the battery's output power,

Ptot = P1 + P2 + P3 + P4

Ptot = (0.021 + 0.0461 + 0.023 + 0.0829 ) W

Ptot = 0.173 W = 0.173 W = Pbat

And that agrees to three significant figures. This agrees with our ideas of energy conservation.

We have calculated all of the currents

Notice, too, that

I1 = I4 = 0.0144 A = (0.0096 + 0.0048) A = I2 + I3
as we would expect from Kirchoff's Jucntion Rule or simply from charge conservation


5. The capacitor is initially uncharged.

a) What is the final charge Qf that will accumulate on the capacitor in this circuit, after switch S is closed, if we wait long enough?
R = 2000
C = 500 µF
V = 12 v

b) What is the time constant of this circuit?
c) What charge will there be on the capacitor 2.0 s after the switch is closed?

 

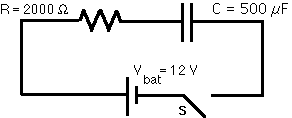
After a long time, the current will be zero because the voltage across the capacitor will just "balance" the voltage of the battery,
Vf = 12 v

C = Q / V

Qf = C Vf

Qf = ( 500 x 10 - 6 F ) ( 12 v )

Qf = 6.0 x 10 - 3 C

The time constant of this circuit is

= RC

= ( 2000 ) (500 x 10 - 6 f )

= 1.0 s

The charge on the capacitor, as a function of time, is

q = q(t) = Qf [ 1 - e - t / ]

q ( 2.0 s) = q (t = 2.0 s) = Qf [ 1 - e - 2.0 / ]

q ( 2.0 s) = Qf [ 1 - e - 2.0 / 1.0 ]

q ( 2.0 s) = Qf [ 1 - ( e - 2 ) ]

q ( 2.0 s) = Qf [ 1 - ( 0.135 ) ]

q ( 2.0 s) = Qf [ 0.865 ]

q ( 2.0 s) = 0.865 Qf

q ( 2.0 s) = 0.865 ( 6.0 x 10 - 3 C )

q ( 2.0 s) = 5.19 x 10 - 3 C

| Return to Calendar |