Circular Motion

Newton's Second Law

applied to a

Banked Curve

How can a car ever travel at all on a slippery highway? Some curves are banked to compensate for slippery conditions like ice on a highway or oil on a racetrack. Below is a car making a banked turn. Without friction, the roadway still exerts a normal force n perpendicular to its surface. And the downward force of the weight w is present. Those two forces add as vectors to provide a resultant or net force F_net which points toward the center of the circle; this is the centripetal force.

Note that this resultant vector -- or net force -- points to the center of the circle; it is not parallel to the banked roadway.

Resolve the forces into their components. Since we are interested in the force that points toward the center of the circle, we choose a coordinate axis that lies along that direction. There is no acceleration in the y-direction so the sum of the forces in the y-direction must be zero.

F_net,y = n cos - w = 0

n cos = w

n = w / cos

F_net,x = n sin

F_c = m v² / r

but

F_c = F_net,x

substituting, this provides

F_c = mv ² / r = n sin = [w / cos ] sin

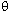
F_c = mv ² / r = w [ sin / cos ]

F_c = mv ² / r = w tan

m v ² / r = m g tan

tan = v ² / g r

This gives the angle necessary for a banked curve that will allow a car to travel in a curve of radius r with constant speed v and require no friction force. A banked curve is designed for one specific speed. If the banked curve is icy so there is no friction force at all then traveling at higher than design speed means the car will slide out, up, and over the edge and traveling at lower than design speed means the car will slide in, down, and off the bank.

At what angle should a curve of 200 m radius be banked so that no friction is required when a car travels at 60 kilometers per hour around the curve?

 

UCM			nonuniform circular motion
Table of Contents

(c) Doug Davis, 2001; all rights reserved