

Ch20; Heat and the First Law of Thermodynamics
Now we can also answer the "Puzzler" question about the pizza.
Cheese is primarily water with a large heat capacity while the crust has very little water and a very small heat capacity.
Homework Solutions
From the fifth edition(!)
Ch20; Questions: 2, 3, 4, 6, 20, *
Ch20; Problems: 1, 3, *, **, ***, ****, 11, (*5), 27, 39, (*6), (*7), (*8), (*9), (*10), 45, (*11)
[Yes, I know I got carried away. Just remember, I have to solve all these, too!
Do not wait and just watch me solve these. Work them out yourself!]
20.Q2 Give one reason why coastal regions tend to have a more moderate climate than inland regions.
Also see Problem 20.10. The specific heat capacity of water is much, much greater than that of air or of dry soil or rocks. Therefore, more heat -- more energy -- is required to change the temperature of water than almost anything else. That means a large body of water changes its temperature far more slowly than most other things. A slowly changing temperature means a moderate climate.
20.Q3 A small crucible is taken from a 2100oC oven and immersed in a tub full of water at room temperature (this process is often referred to as quenching). What is the approximate final equilibrium temperature?
The specific heat capacity of water is large. And we can use a large tub of water. Both of those means we can have a heat capacity of the water that is much greater than that of the crucible. That means the final temperature will be fairly near the initial temperature of the water. The water will increase in temperature -- but only a litt.e
20.Q4 What is the major problem that arises in measuring specific heats if a sample with a temperature above 100oC is placed in water?
If some of the water gets a temperature of 100 degrees (Celsius), it will boil.
20.Q6 The pioneers found that a large tub of water placed in a storage cellar would prevent their food from freezing on really cold nights. Explain why this is so.
Plain water freezes at a higher temperature than that req'd to freeze most food. As the temperature in a cellar starts to go down, heat will be used to freeze the water into ice at zero degrees as long as there is water available before the temperature goes below zero degrees (Celsius). Only when all the water is frozen into ice will the temperature go lower -- and, thus, freeze the food.
20.Q19 In an experimental house, Styrofoam beads were pumped into the air space between the double windows at night in the winter and pumped out to holding bins during the day. How would this assist in conserving heat energy in the house?
Styrofoam beads between the double windows offers good insulation -- the beads prevent the convection circulation currents that would carry heat from the inside to the outside. A heavy curtain does some of this same insulating.
20.Q* Why can you get a more severe burn from steam at 100oC than from water at 100oC?
Steam has much greater internal energy because energy had to be added to the water to vaporize it into steam.
20.1 Water at the top of Niagra Falls has a temperature of 10oC. If it falls through a distance of 50 m and all of its potential energy goes into theating the water, calculate the temperature of the water at the bottom of the falls.Consider some mass M of water, initially at the top of Niagra Falls;
PE = M g h PE = M (9.8 m/s2)(50 m)
PE = 490 M m2/s2
PE = 490 M J/kg
Now, use all of that energy to increase the temperature of the water,
PE = Q = c M T
PE =(4186 J / kg-Co) M
T
490 M J/kg =(4186 J / kg-Co) M
T
490 J/kg =(4186 J / kg-Co)
T
(4186 J / kg-Co)
T =490 J/kg
T = (490 /4186) Co
T = 0.12 Co
20.3 The temperature of a silver bar rises by 10.0 Co when it absorbs 1.23 kJ of heat. The mass of the bar is 525 g. Determine the specific heat of silver.
Q = c m T
c = Q / m
T
c = (1.23 x 103 J)/[(0.525 kg)(10 Co)]
c = 234 J/kg-Co
20.* If 100 g of water at 100oC is poured into a 20-g aluminum cup containing 50 g of water at 20oC, what is the equilibrium temperature of the system?
We will call the final temperature -- the equilibrium temperature -- Tf.
First, consider the hot water;
Th = Tf - Ti = Tf - 100oC
Qlost = Cw mh
Th
Qlost = Cw mh (Tf - 100oC)
Qlost = (4186 J/kg-Co) (0.100 kg) (Tf - 100oC)
Qlost = (418.6 J/Co) Tf - 41,860 J
Now, the aluminum cup;
TA = Tf - Ti = Tf - 20oC
QAl = CAl mAl
TAl
QAl = (900 J/kg-Co) (0.020 kg) (Tf - 20oC)
QAl = 18 Tf J/Co - 360 J
Don't forget the cold water,
Tc = Tf - Ti = Tf - 20oC
Qc = cw mc
Tc
Qc = (4186 J/kg-Co) (0.050 kg) (Tf - 20oC)
Qc = (209.3 J/Co) Tf - 4186 J
Qgain, the total heat gained is the sum of QAl, the heat gained by the aluminum can, and Qc, the heat gained by the cold water,
Qgain = QAl + Qc Qgain = [18 Tf J/Co - 360 J] + [(209.3 J/Co) Tf - 4186 J]
With the way we have defined the temperature change,
T = Tf - Ti
The sum of the heat lost and the heat gained must be zero,
Qlost + Qgain = 0 (418.6 J/Co) Tf - 41,860 J + [18 Tf J/Co - 360 J] + [(209.3 J/Co) Tf - 4186 J] = 0
(418.6 1/Co) Tf - 41,860 + [18 Tf 1/Co - 360 ] + [(209.3 1/Co) Tf - 4186 ] = 0
(418.6 + 18 + 209.3) (1/Co) Tf - (41,860 + 360 + 4186) = 0
645.9 Tf (1/Co) - 46,406 = 0
645.9 Tf (1/Co) = 46,406
Tf = (46,406/645.9) oC
Tf = 71.8 o C
Always ask if this (or any other) answer is "reasonable" or "possible" or "expected". What about Tf = 71.8oC? That is less than the higher temperature and greater than the lower temperature. So that means it is plausible. We had more water at the higher temperature (100oC) than at the lower temperature (20oC) and this final temperature is closer to that higher temperature. So that, too, makes this "believable".
20.** What is the final equilibrium temperature when 10 g of milk at 10oC is added to 160 g of coffee at 90oC? (Assume the heat capacities of the two liquids are the same as that of water, and neglect the heat capacity of the container).
This one, 20.7, should be simple and straightforward after the previous problem, 20.6.
Q = c m T
T = Tf - Ti
Qcoffee + Qmilk = 0
Qcoffee = c mcoffee
Tcoffee
Qcoffee = (4186 J/kg-Co) (0.160 kg) (Tf - 90oC)
Qcoffee = 670 Tf (J/Co) - 60,287 J
Qmilk = c mmilk
Tmilk
Qmilk = (4186 J/kg-Co) (0.010 kg) (Tf - 10oC)
Qmilk = 41.9 Tf (J/kg-Co) - 418.6 J
Qcoffee + Qmilk = 0
[670 Tf (J/Co) - 60,287 J] + [41.9 (J/kg-Co) - 418.6 J] = 0
(670 + 41.9) Tf (J/Co) - (60,287 + 418.6) J = 0
(711.9) Tf (1/Co) - (60,706) = 0
711.9 Tf (1/Co) = 60,706
Tf = (60,706 / 711.9) oC
Tf = 85.3oC
As with the previous problem, always ask if this (or any other) answer is "reasonable" or "possible" or "expected". What about Tf = 85.3oC? That is less than the higher temperature and greater than the lower temperature. So that means it is plausible. We had more water (or coffee) at the higher temperature (90oC) than water (or milk) at the lower temperature (10oC) and this final temperature is much closer to that higher temperature. So that, too, makes this "believable".
20.*** (a) A calorimeter contains 500 ml of water at 30oC and 25 g of ice at 0oC. Determine the final temperature of the system.
(b) Repeat part (a) if 250 g of ice is initially present at 0oC.
This is somewhat similar to the previous problem, 20.7, except we have to take care of a change of state -- due to the melting of the ice -- as well as a temperature change.
Qwater + Qice = 0 Qwater = cw mw
T
Qwater = (4186 J/kg-Co) (0.500 kg) (Tf - 30oC)
Qwater = 2093 Tf (J/Co) - 62,790 J
Now, how much heat is gained by the ice? Does all of the ice melt? We do not know. So we must make an assumption -- or a guess. We then have to see if our result is consistent with that assumption.
Assumption: All the ice melts and Tf > 0oC
Be sure to check for consistency with our final answer and this assumption.
This ice is initially at 0oC so heat that it gains immediatly starts to melt the ice. Remember, mice = m2 = 25 g = 0.025 kg. m2 is the mass of the ice after it has melted and is water at 0oC.
Qice = Qmelt + Qraise Qice = mice L + c m2
T
Qice = (0.025 kg)(3.33 x 105 J/kg) + (4186 J/kg-Co) (0.025 kg) (Tf - 0oC)
Qice = (0.025)(3.33 x 105 J) + (4186 J/Co) (0.025 kg) Tf
Qice = 8,325 J + 105 Tf (J/Co)
Qwater + Qice = 0
[2093 Tf (J/Co) - 62,790 J] + [ 8,325 J + 105 Tf (J/Co)] = 0
(2093 + 105) Tf (J/Co) - (62,790 - 8,325) J= 0
2198 Tf (J/Co) - 54,465 J= 0
2198 Tf (J/Co) = 54,465 J
Tf = (54,465 / 2198) oC
Tf = 24.8oC
Is that "believeable" or "reasonable"? It is between the lowest and highest initial temperature so that means it is, at least, "possible". Yes, I think that seems reasonable.
Now, let's put MORE ice in. This seems like EXACTLY the same problem but with a different value for the mass of the ice. Let's see what happens this time!
Qwater + Qice = 0 Qwater = cw mw
T
Qwater = (4186 J/kg-Co) (0.500 kg) (Tf - 30oC)
Qwater = 2093 Tf (J/Co) - 62,790 J
Now, how much heat is gained by the ice? Does all of the ice melt? We do not know. So we must make an assumption -- or a guess. We then have to see if our result is consistent with that assumption.
Assumption: All the ice melts and Tf > 0oC
Be sure to check for consistency with our final answer and this assumption.
This ice is initially at 0oC so heat that it gains immediatly starts to melt the ice. Remember, this time mice = m2 = 0.250 kg = 250 g. m2 = 0.250 kg is the mass of the water that has melted whose temperature changes from 0oC to the final temperature Tf.
Qice = Qmelt + Qraise Qice = mice L + c m2
T
Qice = (0.250 kg)(3.33 x 105 J/kg) + (4186 J/kg-Co) (0.250 kg) (Tf - 0oC)
Qice = (0.250)(3.33 x 105 J) + (4186 J/Co) (0.250 kg) Tf
Qice = 83,250 J + 1046 Tf (J/Co)
Qwater + Qice = 0
[2093 Tf (J/Co) - 62,790 J] + [ 83,250 J + 1046 Tf (J/Co)] = 0
(2093 + 1046) Tf (J/Co) - (62,790 - 83,250) J= 0
3139 Tf (J/Co) - 61,957.5 J= 0
3139 Tf (J/Co) + 20,460 J= 0
Tf = - (20,460 / 3139) oC
Tf = - 6.5oC
Again, we need to ask if this is "believeable" and I think this seems "believeable". This answer is NOT "believeable". It is lower than our lowest initial temperature. And it is inconsistent with our assumption that all the ice melts and Tf >0oC.
Now what do we do?
We make a new assumption.
Assumption: Not all of the ice melts. This means Tf = 0. How much ice does melt? We don't know so we will just call it Mmelt and solve for that (and see if Mmelt , 0.250 kg).Qwater + Qice = 0 Qwater = cw mw
T
Qwater = (4186 J/kg-Co) (0.500 kg) (Tf - 30oC)
Qwater = (4186 J/kg-Co) (0.500 kg) (0 - 30oC)
Qwater = - 62,790 JRemember, we know the final temperature; Tf = 0oC
This ice is initially at 0oC so heat that it gains immediatly starts to melt the ice. Remember, this time when some of the ice melts it does not change its temperature since Tf = 0oC. We are now looking for Mmelt .
Qice = Qmelt + Qraise Qice = Mmelt L
Qice = (Mmelt)(3.33 x 105 J/kg)
Qwater + Qice = 0
- 62,790 J + (Mmelt)(3.33 x 105 J/kg) = 0
(Mmelt)(3.33 x 105 J/kg) = 62,790 J
Mmelt = [62,790 / 3.33 x 105 ] kg
Mmelt = 0.188 kg
Mmelt = 188 gAs always, ask if this is "believeable" or "reasonable" -- or consistent with our assumptions. Yes, this is consistent with our assumption of only part of the ice melting. This amount of ice that melts is, indeed, less than our total, initial amount of ice. So this answer seems plausible to me.
20.**** The air temperature above coastal areas is profoundly influenced by the large specific heat of water. One reason is that the heat released when one cubic meter of water cools by 1.0 Co will raise the temperature of an enormously larger volume of air by 1.0 Co. Estimate this volume of air.
The specific heat of air is approximately 1.0 kJ/kg-Co. Take the density of air to be 1.25 kg/m3.
Qair = Qwater
Q = c mT
T = 1 Co
Qair = cair mair (1 Co)
Qair = (1.0 kJ/kg-Co) mair (1 Co)
Qwater = cwater mwater (1 Co)
cwater = 4186 J/kg-Co = 4.186 kJ/kg-Co
mwater = 1 m3 x 1000 kg/m3
Qwater = (4.186 kJ/kg-Co) (1 m3 x 1000 kg/m3) (1 Co)
Qwater = 4186 kJ
Qair = (1.0 kJ/kg-Co) mair (1 Co) = 4186 kJ
mair = 4186 kJ / [(1.0 kJ/kg-Co) (1 Co)]
mair = 4186 kgThat's a very large mass of air. But we want the volume of the air.
Vair = 4186 kg / [1.25 kg/m3]
Vair = 3,429 m3
20.11 A water heater is operated by solar power. If the solar collector has an area of 6.0 m2 and the power delivered by sunlight is 550 W/m2, how long does it take to increase the temperature of 1.0 m3 of water from 20oC to 60oC?
Q = c m T
m = (1.0 m3)(1000 kg/m3) = 1000 kg
Q = (4186 J/kg-Co)(1000 kg)(40 Co)
Q = 1.67 x 108 J
Q = E = P twhere t is time
t = E / P
P = [550 W/m2][6.0 m2]
P = 3300 W
t = [1.67 x 10 J]/[3300 W]
t = 50,740 [J/W]Now, what in the world is a [J/W]? I certainly hope that's a second. But let's find out for sure --
t = 50,740 [J/W][1W / (J/s) ]
t = 50,740 s
t = 50,740 s [1 min / 60 s]
t = 846 min[1 h / 60 min]
t = 14.1 hAnd that's all day -- on a sunny, summer day!
20.(*5) If 90.0 g of molten lead at 327.3oC is poured into a 300.0-g casting made of iron initially at 20.0oC, what is the final temperature of the sytem? (Assume there are no heat losses.)
Qlost + Qgain = 0 Qlost = QPb = mPB LPB + cPb mPb
TPb
Remember, we're starting with molten lead and we're going to turn it into solid lead and then lower its temperature. Lead fuses into a solid at 327.3oC. Or we could say the melting point of lead is 327.3oC. We can also say the "freezing point" of lead is 327.3oC. Anyway, we are starting with molten lead just at its freezing/melting/fusing point. That means we do not need the change the temperature of the molten lead. But we do have to change the temperature of the lead immediately after it fuses into a solid.
Qlost = QPb = (0.090 kg)(2.45 x 104 J/kg) + + (128 J/kg-Co)(0.090 kg)(Tf - 327.3oC)
Qlost = QPb = 2205 J + 11.5 Tf (J/kg-Co) - 3,770 J
Qgain = QFe = cFe mFe
TFe
Qgain = QFe = (448 J/kg-Co)(0.300 kg)(Tf - 20.0oC)
Qgain = QFe = 134.4 Tf (J/kg-Co) - 2,688 J
Qlost + Qgain = 0
[ 2205 J + 11.5 Tf (J/kg-Co) - 3,770 J] + [134.4 Tf (J/kg-Co) - 2,688 J] = 0
[(11.5 + 134.4) Tf (J/kg-Co)] - [ - 2205 + 3,770 + 2,688] J = 0
145.9 Tf (J/kg-Co) - 4,253J = 0
145.9 Tf (J/kg-Co) = 4,253 J
Tf = (4,253/146)oC
Tf = 29.1oC
Is that what we might expect? It is between the two initial extreme temp's so it is certainly "possible". There is a lot more of the iron casting than of the molten lead and this temperature is closer to the initial temp of the iron. So I think this seems "reasonable".
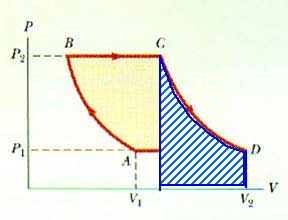
20.27 A gas expands from I to F along three possible paths as indicated by Figure P20.29. Calculate the work in joules done by the gas along the paths IAF, IF, and IBF.
Along path IAF,
the work done is the area under the curve,
W = P V
W = (4 atm)(2 L)
W = 8 L-atm
Now, what's a liter-atmosphere? We solved for that in the last chapter. But let's do it again here. 1.0 atm = 1.013 x 10 + 5 Pa = 1.013 x 10 5 N/m2
1 L-atm = 1 L-atm [ 10 - 3 m3 / L] [(1.013 x 105 N/m2) / atm] 1 L-atm = 101.3 N-m = 101.3 J
W = 8 L-atm [101.3 J/L-atm]
W = 810.4 J
Along path IBF,the work done is still the area under the curve. Now we can describe that as the area of the rectangle BFDA plus the area of the triangle IBF.
W = ABFDA + AIBF W = (1 atm)(2 L) + (1/2)(3 atm)(2 L)
W = 5 L-atm
W = 5 L-atm [101.3 J/L-atm]
W = 506.5 J
Along path IAF,There is no work done along the path IB; this is a constant volume process (this is also known as an isometric process). Along path BF, there is work done.
Wtot = WIB + WBF Wtot = 0 + 2 L-atm
Wtot = 2 L-atm
Wtot = 202.6 J
20.39 An ideal gas undergoes a thermodynamic process that consists of two isobaric and two isothermal steps as shown in Figure P20.32. Show that the net work done during the four steps is
Wnet = P1 (V2 - V1) ln (P2/P1)
Find the amount of work done along each piece of the process.
[Incidently, this diagram is not drawn correctly. These isotherms look almost parallel to each other and they are not -- or should not be! This may influence your intuition. A better diagram might look like this:
Let's begin by labeling the temperatures of the two isotherms:
Start with the path from A to B. Remember, this is an isotherm:

WAB = n R T ln[VB/VA]
Look at state A, where V = VA = V1 and P = P1 and T = T1. There, the ideal gas law
P V = n R T becomes
P1 V1 = n R T1 or
TAB = T1 = P1 V1 / n R Remember, this is an isotherm so T = T1 = TA = TB = TAB is a constant all along this process.
We need to evaluate VB = Vf; something like this almost always means using the ideal gas law:
Vf = VB = n R T1/P2 Vf = VB = n R (P1 V1 / n R)/P2
Vf = VB = P1 V1/P2
Vf = VB = V1 (P1/P2)
WAB = n R T ln [VB/VA]
WAB = n R T1 ln [V1 (P1/P2)/V1]
WAB = n R T1 ln [P1/P2]
WAB = n R (P1 V1 / n R) ln [P1/P2]
WAB = P1 V1 ln [P1/P2]
WAB = P1 V1 ln [P1/P2]
Next, from B to C. This should be easy because it's an isobar:
or

WBC = P
V
WBC = P2 (VC - VB)
We have already solved for VB,
VB = V1 (P1/P2) Now we can use the isotherm from C to D to solve for the final volume VC. Along this isotherm, T = TC= TD = TCD = T2; the temperature is a constant.
P V = n R T PC VC = n R TC
VC = n R TC/PC
VC = n R T2/P2
We can make a substitution for T2 by looking at state D,
P1 V2 = n R T2 T2 = P1 V2 / n R
Then
VC = n R (P1 V2 / n R)/P2 VC = P1 V2/P2
VC = V2 (P1/P2)
[ Perhaps a more direct method might be
P V = n R T at state C,
PC VC = n R TC P2 VC = n R T2
at state D,
PD VD = n R TD P1 V2 = n R T2
P2 VC = n R T2 = P1 V2
VC = P1 V2/P2
VC = V2 (P1/P2)
Either way, of course, the result is the same for VC].
VC = V2 (P1/P2) WBC = P2 (VC - VB)
WBC = P2 [V2 (P1/P2) - V1 (P1/P2)]
WBC = P2 [V2 - V1] (P1/P2)
WBC = P1 [V2 - V1]
Then from C to D; another isotherm:
WCD = n R T ln[VD/VC]
Look at state D, where V = VD = V2 and P = P1 and T = T2. There, the ideal gas law
P V = n R T becomes
P1 V2 = n R T2 or
TCD = T2 = P1 V2 / n R
Remember, this is an isotherm so T = T2 = TC = TD = TCD is a constant all along this process.
We already know Vf = VD = V2. We need to evaluate Vi = VC; as always, this means using the ideal gas law:
Vi = VC = n R T2/P2 Vi = VC = n R (P1 V2 / n R)/P2
Vi = VC = P1 V2/P2
Vi = VC = V2 P1/P2
[ It may be useful to evaluate this in a different method.
At state C, we can write
P V = n R T P2 VC = n R T2
At state D, we can write
P1 V2 = n R T2 P2 VC = n R T2 = P1 V2
VC = P1 V2 / P2
VC = V2 (P1/P2)
Of course that is the same result.]
WCD = n R T ln [Vf/Vi] WCD = n R T ln [VD/VC]
WCD = n R T ln [V2/(V2 P1/P2)]
WCD = n R T2 ln [P2/P1]
WCD = n R ( P1 V2 / n R) ln [P2/P1]
WCD = P1 V2 ln [P2/P1]
WCD = P1 V2 ln [P2/P1]
And, finally, from D back to A; another isobar:

WDA = P1
V
WDA = P1 (V1 - V2)
Caution:
V = Vfinal - Vinitial. Or, remember that this is a compression so the work done by the system will be negative!
Now we have calculated all the pieces. The total or net work done should just be the sum of all of these individual processes. That is,
WAB = P1 V1 ln [P1/P2] WBC = P1 [V2 - V1]
WCD = P1 V2 ln [P2/P1] = - P1 V2 ln [P1/P2]
WDA = P1 [V1 - V2]
Wnet = WAB + WBC + WCD + WDA
Wnet = P1 V1 ln [P1/P2] + P1 [V2 - V1] - P1 V2 ln [P1/P2] + P1 [V1 - V2]
Wnet = P1 V1 ln [P1/P2] - P1 V2 ln [P1/P2]
Wnet = P1 (V1 - V2) ln [P1/P2]
Wheeeeeew!
20.(*6) A sample of ideal gas is expanded to twice its original volum of 1.0 m3 in a quasi-static process for which P = a V2, with a = 5.0 atm/m6, as shown in Figure P20.33. How much work was done by the expanding gas?
How much work was done by the expanding gas?
Mixed message: The units are always important. Esp'ly in situations like Heat and Thermo, where there may be mixed units, it is important to be sure you have consistent units. You can always carry the units through until the end -- as I have done here. You can also stop someplace along the way and ensure that all the units you have are consistent. But never, never, never just ignore the units and hope or expect that they will, indeed, come out alright.
20.(*7) A gas is compressed at a constant pressure of 0.80 atm from 9.0 L to 2.0 L. In the process, 400 J of thermal energy leaves the gas.
(a) What is the work done by the gas?
"at constant pressure" means "isobaric" or
W = P V
W = (0.80 atm) (2.0 L - 9.0 L)
W = - 5.6 L-atm
The negative sign means work is done to the system (or the system does negative work on its surroundings). Now, what is a L-atm?
W = - 5.6 L-atm [(1.013 x 105 N/m2)/(atm)] [(10 - 3 m3)/L] W = - 1.7 x 103 N-m
W = - 1.7 x 103 J
W = - 1,700 J
(b) What is the change in its internal energy?
Q = W + U
U = Q - W
Q = - 400 J
U = ( - 400 J) - ( - 1,700 J)
U = 1,300 J
The internal energy increases. The gas has been compressed or work has been done to the gas; that would increase its internal energy. Some heat has flowed out of the gas; that would decrease its internal energy. But the increase (due to the compression) is greater than the decrease (due to the heat loss).
20.(*8) Five moles of an ideal gas expands isothermally at 127oC to four times its intiial volume. Find --
(a) the work done by the gas and
For an isothermal expansion, we already have seen that the work done is
Now we just need to find plug in the numbers. We know all the pieces;
n = 5 T = 127oC = 400 K
Vf = 4 Vi
W = (5) (8.315 J / mole-K) (400 K) ln[4]
W = (5) (8.315) (400) (1.39) J
W = 23,054 J
W = 23,000 J
(b) the thermal energy transferred to the system;
Q = W + U
But the internal energy is a function of the temperature. Since this is an isothermal process, the internal energy remains constant (along with the temperature). That is,
U = 0
Q = W
Q = 23,000 J
This means that 23,000 J of energy flows into the system and causes the system to expand and to do 23,000 J of work on its surroundings.
put both in units of joules.
20.(*9) An ideal gas initially at 300 K undergoes an isobaric expansion at 2.50 kPa. If the volume increases from 1.00 m3 to 3.00 m3 and 12.5 kJ of thermal energy is transferred to the gas, find
(a) the change in its internal energy and
For an isobaric expansion,
W = P V
W = (2.5 kPa) (3 - 1) (m3)
W = (2.5 kPa) (2) (m3)
W = 5 kPa-m3
W = 5 x 103 Pa-m3
W = 5 x 103 (N/m2)(m3)
W = 5 x 103 N-m
W = 5 x 103 J
W = 5 kJ
And we know
Q = 12.5 kJ Q = W +
U
U = Q - W
U = 12.5 kJ - 5 kJ
U = 7.5 kJ
(b) its final temperature.
P V = n R T P = n R T / V
P = n R T1/V1 = n R T2/V2 = constant
T2/V2 = T1/V1
T2 = T1 (V2/V1)
Tf = Ti (Vf/Vi)
Tf = 300 K (3 m3/1 m3)
Tf = 900 K
20.(*10) Helium with an initial volume of 1.00 liter and an initial pressure of 10.0 atm expands to a final volume of 1.00 m3. The relationship between pressure and volume during the expansion is PV = constant. Determine . . .
(a) the value of the constant,
P V = constant P V = (1 L) (10 atm)
P V = constant = 10 L-atm
(b) the final pressure, and
Pf Vf = Pi Vi Pf = Pi (Vi/Vf)
Pf = (10 atm) (1 L/1 m3)
1 m3 = 1,000 L
Pf = 10 atm (1 L / 1,000 L)
Pf = 0.01 atm
(c) the work done by the helium during the expansion.
P V = const = 10 L-atm P = (10 L-atm) / V
W = (10 L-atm) [ ln Vf - ln Vi ]
W = (10 L-atm) ln [Vf/Vi]
W = (10 L-atm) ln [1.0 m3/1.0 L]
W = (10 L-atm) ln [1,000 L/1.0 L]
W = (10 L-atm) ln [1,000]
W = (10 L-atm) (6.91)
W = 69.1 L-atm
We know that a L-atm is, indeed, a unit of work. But we are more familiar with work being expressed in units of joules.
W = 69.1 L-atm [ 0.001 m3/L][(1.013 x 105 N/m2)/atm] W = 7,000 J
W = 7 kJ
20.45 A bar of gold is in thermal constanct with a bar of silver of the same length and area (as shown in Figure P20.55). One end of the compound bar is maintained at 80.0oC while the opposite end is at 30.0oC. When the heat flow reaches steady state, find the temperature at the junction.
Call the temperature of the center -- where the two bars are joined -- Tc,
HAu = Hgold = KAu A (80oC - Tc ) / L HAg = Hsilver = KAg A (Tc - 30oC) / L
HAu = HAg
KAu A (80oC - Tc ) / L = KAg A (Tc - 30oC) / L
KAu (80oC - Tc ) = KAg (Tc - 30oC)
KAu 80oC - KAu Tc = KAg Tc - KAg 30oC
KAg Tc + KAu Tc = KAu 80oC + KAg 30oC
(KAg + KAu) Tc = KAu 80oC + KAg 30oC
Tc = [KAu 80oC + KAg 30oC]/(KAg + KAu)
Tc = [(314 W/mCo)(80oC) + (427 W/mCo)(30oC)] / (314 W/mCo + 427 W/mCo)
Tc = [(314)(80oC) + (427)(30oC)] / (314 + 427)
Tc ={ [(314)(80) + (427)(30)] / (314 + 427)}oC
Tc = 51.2oC
Is this a reasonable answer? It is between the low temperature (30oC) and the high temperature (80oC) so that seems believeable. Gold is also a better conductor than silver so the temperature Tc ought to be closer to the gold's extreme temperature (30oC) than to the silver's extreme temperature (80oC); and that is the case.
20.(*11) The brick wall (k = 0.8 W/m-Co) of a building has dimensions of 4.0 m x 10.0 m and is 15 cm (0.15 m) thick. How much heat (in joules) flows through the wall in a 12-h period when the average inside and outside temperatures are, 20oC and 5oC, respectively?
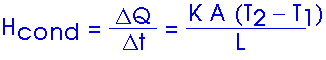
Hcond = [(0.8 W/m-Co)(40 m2)(15 Co)]/0.15 m
Hcond = 3,200 W
Hcond = 3,200 J/s
Q = [3,200 J/s] [12 h] [3,600 s/h]
Q = 1.38 x 108 J
(c) Doug Davis, 2002; all rights reserved
Ch21;
Return to Ch20 ToC