

Kinetic Theory of Gases
Homework Solutions From the FIFTH edition
Questions: 1, 2, 4, 6, 12, 15
Problems: *, 3, **, 8, 13, ****, 25, *****, ******, 33
Be sure and do these; do not just wait and watch me do them in class!
Q21.1 Dalton's law of partial pressures states: The total pressure of a mixture of gases is equal to the sum of the partial pressures of gases making up the mixture. Give a convincing argument of this law based on the kinetic theory of gases.
Pressure is a result of atoms (or molecules) bombarding the sides of
the container. If there are more atoms in the container, there will be
more bombarding the sides of the container and this will increase the pressure. Dalton's law that the total pressure is the sum of the partial pressure is another way of saying the total force or pressure due to the sum of all the atoms hitting the side of the container is the sum of the force or pressure due to the different kinds of atoms hitting the side of the container.Q21.2 One container is filled with helium gas and another with argon gas. If both containers are at the same temperature, which molecules have the higher rms speed?
At the same temperature, the average value of the translational kinetic energy [(1/2) m <v2>] will be the same for both helium and argon. Argon has a larger mass so it will have a smaller value of <v2> or vrms. Helium has a smaller mass so it will have a larger value of <v2> or vrms.
Q21.4 Although the average speed of gas molecules in thermal equilibrium at some temperature is greater than zero, the average velocity is zero. Explain.
The average velocity must be zero since the center of mass of the gas is not moving.Q21.6 A liquid partially fills a container. Explain why the temperature of the liquid decreases when the container is partially evacuated. (It is possible to freeze water using this technique.)
The faster-moving atoms are the ones that escape from the liquid's
surface (that is, they are the ones that evaporate). That means the
average speed of the remaining atoms is decreased -- and the
temperature decreases as the average speed of the atoms decreases.Q21.12 Why does a diatomic gas have a greater thermal energy content per mole than a monatomic gas at the same temperature?
The molar specific heat of a diatomic molecule is CV = (5/2) R, meaning U = (5/2) n R T, while, for a monatomic gas, CV = (3/2) R or U = (3/2) n R T. Since the molar specific heat is greater for a diatomic molecule, there is more internal energy stored inthe motion of the molecules for the same temperature than for that temperature in a monatomic gas.Q21.13 An ideal gas is contained in a vessel at 300 K. If the temperature is increased to 900 K,
(a) by what factor does the rms speed of each molecule change?
The temperature has increased by a factor of 3. The rms speed goes like the square root of the temperature so we have increased the rms speed by SQRT(3)=1.732(b) by what factor does the pressure in the vessel change?
The Ideal Gas Law still holds, P V = n R T. If the volume remains constant, an increase in temperature by a factor of 3 means an increase in pressure by the same factor of 3.
SQRT[] means "Square Root of" because it is easier for me to write SQRT than to go to a graphics editor and construct a Square Root sign.
21.*. Find the rms speed of nitrogen molecules under standard conditions, 0.0oC and 1.00 atm pressure. Recall that 1 mole of any gas occupies a volume of 22.4 liters under standard conditions.
Eq 21.7, on page 590, tells us
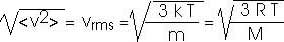
T = 0oC = 273 K
R = 8.31 J / mol-K
M = 28 g/mole = 28 x 10 - 3 kg/mole
vrms = SQRT[ 3 (8.31 J/mol-K)(273 K)/(28 x 10 - 3 kg/mole)]
vrms = SQRT [2.43 x 105 (J/mol-K)(K)/(kg/mole)]
vrms = SQRT [2.43 x 105 (J/kg)(N-m/J)(kg-m/s2/N)]
vrms = SQRT [2.43 x 105 (m2/s2)]
vrms = 493 m/s
Be careful with the units. They're important! They're not just an afterthought.
21.3 In a 30-s interval, 500 hailstones strike a glass window of area 0.60 m2 at an angle of 45o to the window surface. Each hailstone has a mass of 5.0 g (0.005 kg) and a speed of 8.0 m/s. If the collisions are elastic, find the average force and pressure on the window.
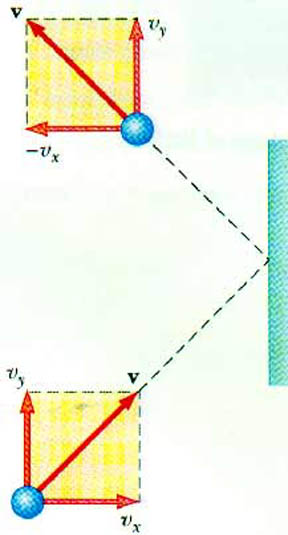
vx = v cos 45o
vx = (8.0 m/s)(0.707) = 5.66 m/s
px = m vx = (0.005 kg)(5.66 m/s) = 2.83 x 10 - 2 kg-m/s
px = 2 px = 5.66 x 10 - 2 kg-m/s
F =
pxtot/
t
F = (500)(5.66 x 10 - 2 kg-m/s)/30 s
F = 0.943 kg-m/s2
F = 0.943 N
P = F/A
P = 0.943 N / 0.60 m2
P = 1.57 N/m2
P = 1.57 Pa
21.** Calculate the rms speed of an H2 molecule at 250oC.
Of course, this is basically the same as problem 21.1 above. But it is always good to work similiar problems -- just to see that the idea is the same even with different numbers. This time
T = 250oC = 523 K M = 2 g/mole = 2 x 10 - 3 kg/mole
As with 21.1, we begin with Eq 21.7, from page 590,
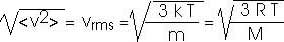
R = 8.31 J / mol-K
vrms = SQRT[ 3 (8.31 J/mol-K)(523 K)/(2 x 10 - 3 kg/mole)]
vrms = SQRT [6.52 x 106 (J/mol-K)(K)/(kg/mole)]
vrms = SQRT [6.52 x 106 (J/kg)(N-m/J)(kg-m/s2/N)]
vrms = SQRT [6.52 x 106 (m2/s2)]
vrms = 2 550 m/s
21.8 If the rms speed of a helium atom at room temperature is 1350 m/s, what is the rms speed of an oxygen (O2) molecule at this temperature? (The molar mass of O2 is 32 and the molar mass of He is 4.)
This problem, too, begins with Eq 21.7,
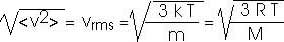
vrmsO/vrmsH = SQRT[3 R T/MO] / SQRT[3 R T/MH]
vrmsO/vrmsH = SQRT[ (3 R T/MO) / (3 R T/MH) ]
vrmsO/vrmsH = SQRT[ MH/MO ]
vrmsO/vrmsH = SQRT[ 4/16 ]
vrmsO/vrmsH = SQRT[ 1/4 ]
vrmsO/vrmsH = 1/2
vrmsO/vrmsH = 0.5
vrmsO = 0.5 vrmsH
vrmsO = 0.5 (1350 m/s)
vrmsO = 675 m/s
21.*** One mole of xenon gas at 20.0oC occupies 0.0224 m3. What is the pressure exerted by the Xe atoms on the walls of a container?
P V = n R T P = n R T / V
P = (1 mole) (8.31 J/mole-K) (293 K) / 0.0224 m3
P = 1.09 x 105 (J/m3)
Now, what in the world is a J/m3?
P = 1.09 x 105 (J/m3) [ N-m / J ] P = 1.09 x 105 N/m2
P = 1.09 x 105 Pa
P = 1.09 x 105 Pa [1 atm / 1.013 x 105 Pa]
P = 0.029 atm
21.13 Calculate the change in internal energy of 3.0 moles of helium gas when its temperature is increased by 2.0 K.
For an ideal gas, we would have
U = (3/2) n R T
U = (3/2) n R
T
U = (3/2) (3 moles) (8.31 J/mole-K) (2.0 K)
U = 74.8 J
While helium behaves very nearly as an ideal gas, we can do this calculation for the actual behavior of helium.
U = n Cv
T
From Table 21.2 on page 647 of the text, we find that, for helium
cv = 12.5 J/mole-K
U = (3 moles)(12.5 J/mole-K)(2.0 K)
U = 75.0 J
21.**** One mole of an ideal monatomic gas is at an initial temperature of 300 K. The gas undergoes an isovolumetric process acquiring 500 J of heat. It then undergoes an isobaric process losing the same amount of heat. Determine (a) the new temperature of the gas and (b) the work done on the gas.
[[ Note: Part of the earlier solution posted on the web was wrong.]]
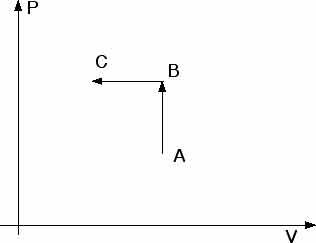
For the isovolumetric (constant volume) process, from A to B, no work is done,
WAB = 0 Q =
U = 500 J
For the isobaric (constant pressure), process, from B to C, the work is
WBC = P
V
We know the initial temperature, TA = 300 K. To find WBC we will need the temperatures TB and TC at states B and C so we can find P
V for the expression above.
QAB = n CV
T = 500 J
(n) ((3/2) R) (
T) = 500 J
(1 mole) ((3/2) 8.31 J/mole-K) (
T) = 500 J
( 12.5 J / K )
T = 500 J
T = (500/12.5) K
T = 40 K
TB = 300 K + 40 K
TB = 340 K
QBC = n CP
T
- 500 J = (n) ((5/2) R) (
T)
- 500 J = (1 mole) ((5/2) 8.31 J/mole-K) (
T)
- 500 J = ( 20.8 J / K )
T
T = - (500/20.8) K
T = - 24.1 K
TC = 340 K - 24.1 K
TC = 315.9 K
Wtot = WAB + WBC
WAB = 0
WBC = P
V
Qtot = Wtot +
Utot
Qtot = 500 J + ( - 500 J) = 0
Wtot = -
Utot
U = n CV
T
U = (n) ((3/2) R) (
Ttot)
T = 40.0 K - 24.1 K
T = 15.9 K
U = (n) ((3/2) R) (
Ttot)
U = (1 mole)(12.5 J/mole-K)(15.9 K)
U = 199 J
Wtot = -
Utot
W = - 199 J
[[ This final answer is the same as was posted earlier but part of the earlier solution was wrong. ]]
21.25 Two moles of an ideal gas (
= 1.40) expands slowly and adiabatically from a pressure of 5.0 atm and a volume of 12.0 liters to a final volume of 30.0 liters.
(a) What is the final pressure of the gas?
"Adiabatically" means
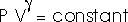
or
Pf = (5.0 atm) (12.0 L/30.0 L)1.4
Pf = (5.0 atm) (0.4)1.4
Pf = (5.0 atm) (0.2773)
Pf = 1.386 atm
(b) What are the initial and final temperatures?
Again (or "as usual"?!?!?), we will find the Ideal Gas Law very useful;
P V = n R T T = P V / n R
Ti = Pi Vi / n R
Ti = (5.0 atm) (12.0 L)/[(2.0 moles) (8.31 J/mole-K)]
Be careful! While that equation is true, it is also clumsy or cumberson since we have such strange or mixed units. Since we have pressure in atmospheres and volume in liters, we will be far better served to use R in units of L-atm instead of joules! Again (and again and again and again!), watch the units! Units are not an "add-on"; they're important -- even vital!
Ti = (5.0 atm) (12.0 L)/[(2.0 moles) (0.0821 L-atm/mole-K)] Ti = 365.4 K
Tf = Pf Vf / n R
Tf = (1.386 atm) (30.0 L)/[(2.0 moles) (0.0821 L-atm/mole-K)]
Tf = 253.2 K
21.***** Four liters of a diatomic ideal gas (
= 1.40) confined to a cylinder are put through a closed cycle. The gas is initially at 1.0 atm and at 300 K. First, its pressure is tripled under constant volume. It then expands adiabatically to its original pressure and finally is compressed isobarically to its original volume.
(z) What is its initial pressure?
P V = n R T P = n R T / V
(a) Draw a PV diagram of this cycle.
Here is a rough sketch:
(b) Determine the volume at the end of the adiabatic expansion.
As we move along the adiabat,
or
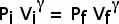
or
(c) Find the temperature of the gas at the start of the adiabatic expansion
At state A,
PA VA = n R TA n = PA VA / R TAA
At state B, the start of the adiabatic expansion,
PB VB = n R TBB TB = PB VB / n R
TB = PB VB /[(PA VA / R TA) R]
TB = TA [ PB VBB /(PA VA) ]
TB = TA (PB/PA) (VB/VA)
[ or, we could have gotten this about as easily by noting
P V = n R T P V / T = n R
PA VA/TA = PB VB/TB
TB = TA (PB/PA) (VB/VA)
Having done this both ways, this way seems noticeably easier. But, of course, the result is the same.]
TB = TA (PB/PA) (VB/VA) Of course,
VB = VA TB = 300 K (3 atm/1 atm) (1)
TB = 300 K (3)
TB = 900 K
(d) Find the temperature at the end of the cycle.
We know the pressure and volume for state C, the end of the adiabatic expansion,
PC = 1 atm VC = 8.77 L
P V = n R T
P V / T = const
PA VA / TA = PC VC / TC
TC = TA (PC/PA) (VC/VA)
TC = 300 K (1 atm/1 atm) (8.77 L/4 L)
TC = 300 K (1) (2.19)
TC = 657.5 K
(e) What was the net work done for this cycle?
Look at the work for each piece and then sum those;
WAB = 0 WBC = -
U
T = Tf - Ti = TC - TB
T = 657.5 K - 900 K
T = - 242.5
U = n CV
T
U = n [ (5/2) R ] [ - 242.5 K ]
How many moles do we have? Go back to state A and find out;
P V = n R T n = [ P V/T ] [1/R]
n = [ 1 atm - 4 L / 300 K] [1/R]
U = [ 1 atm - 4 L / 300 K] [1/R] [ (5/2) R ] [ - 242.5 K ]
U = [ 4 atm - L / 300 ] [ (5/2)] [ - 242.5 ]
U = - 8.08 L-atm
We have done this unit coversion before. We could just go back and get it. But it's worth doing from "scratch", too;
U = - 8.08 L-atm [0.001 m3/L] [1.013 x 105 (N/m2)/atm]
U = - 819 J
WBC = + 819 J
WCA = P
V
WCA = (1 atm) (4 L - 8.77 L)
WCA = - 4.77 L-atm
WCA = - 4.77 L-atm [0.001 m3/L] [1.013 x 105 (N/m2)/atm]
WCA = - 483 J
Wtot = WAB + WBC + WCA
Wtot = 0 + 819 J - 483 J
Wtot = 336 J
While I have labeled this Wtot, as in the total work, we could also call this the net work and label it Wnet.
21.****** A 5.0-liter vessel contains 0.125 mole of an ideal gas at 1.50 atm. What is the average translational kinetic energy of a single molecule?
<KE> = (1/2) m <v2> <KE> = (1/2) m <v2> = (1/2) k T
So, first, we must find the temperature T
P V = n R T T = P V / n R
T = (1.5 atm) (5.0 L) / [(0.125 mole) (0.0821 L-atm/mole-K)]
T = 731 K
<KE> = (1/2) k T = (1/2) (1.38 x 10 - 23 J/K) (731 K)
<KE> = 5.04 x 10 - 21 J
21.33 Consider 2.0 moles of an ideal diatomic gas. Find the total heat capacity at constant volume and at constant pressure if
(a) the molecules rotate but do not vibrate and
CV = (5/2) R Ctot = n CV = 5 R
(b) the molecules rotate and vibrate.
CV = (7/2) R Ctot = n CV = 7 R
(c) Doug Davis, 2002; all rights reserved
Return to Ch21 ToC