General Physics II

Consider the electric potential due to a point charge q, As we move from point A, at distance r_A from the charge q, to point B, at distance r_B from the charge q, the change in electric potential is

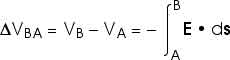
Remember, the little "caret" or "hat" over the vector r means this is a unit vector -- it points in the radial direction and has a magnitude of one.

Only the radial distance r determines the work done or the potential. We can move through any angle we like and, as long as the radial distance remains constant, no work is done or there is no change in the electric potential.

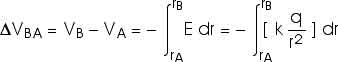
This is the change in electric potential due to a point charge as we move from r_A to r_B.

We could ask about the change in electric potential energy as we move a charge q' from radius r_A to r_B due to a point charge q,

As with gravitational potential energy, it is more convenient -- and, therefore, useful -- to talk about the electric potential energy or the electric potential relative to some reference point. We will choose that reference point to be infinity. That is,

That means we can then write the electric potential at some radius r as

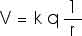
If we bring in a charge q', a distance r, from charge q, it (or "the system") will have electric potential energy of

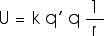
Here are charges q₁ and q₂, a distance r₁₂ apart. Their electric potential energy is

That is, that much work is required to bring these two charges in from infinitly far away to this present distance of r₁₂ apart. Think of bringing q₁ in initially. With no other charges around, no work is required. Now, with q₁ in place, bring in charge q₂ from infinity to r₁₂. The work required is now stored up as electric potential energy. Of course we can talk about the "point in space" located at distance r₁₂ from charge q₁ and talk about the electric potential at that point.

Remember, energy is a scalar. Electric potential is a scalar.

We have equations to tell us the electric potential energy of two charges or the electric potential at a point in space because of one electric charge. What if we have more than one electric charge?

That is, the total or net electric potential is the scalar sum of the electric potential due to each of the individual point charges q_i.

| Numerical Example - electric potential energy |

| Numerical Example - electric potential |

There are no navigational links from these Numerical Examples to get BACK to this page. You will have to use BACK or GO from your internet browser.

Electric Potential

Electric Potential due to a Point Charge