Second Hour Exam
for
PHY 1361
March 8, 2002
Equation sheet
F = k Qq/r2
E = F/q
E = k Q/r2
V = U/q
V = k Q/r
k = 9 x 109 N-m2/C2
k = 1/4 

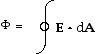
 = Q/
= Q/
E = k Q/r2
E = k [Q/a3] r
E = 2 k  /r
/r
E =  /2
/2 
E =  V/
V/ s
s
C = Q/V
Ceq = C1 + C2 + C3
1/Ceq = 1/C1 + 1/C2
+ 1/C3
U = (1/2) Q V = (1/2) C V2
= (1/2) Q2/C
| Return
to Calendar |
Second Hour Exam
for
PHY 1361
March 8, 2002
Name:
1. __________
2. __________
3. __________
4. __________
CQ ________
Total __________
Again, pace yourself . Don’t spend too much time on one problem.
Write what you know and go on to another problem. If you have time, you can
come back and think more about a problem. I can’t give partial credit for
a blank page.
Calculus is important. I chose to use the parallels with problems 1
and 2 describing electric field and electric potential.
This choice left insufficient time for a good calculus problem.
Such a calculation from an extended charge distribution will surely appear on
the final.
Give a sigh of relief and enjoy your Spring Break!
| Return
to Calendar |
1. Charges q1, q2, and q3 have the values
and locations shown here. What is the electric field (magnitude and
direction) at point P as shown here?
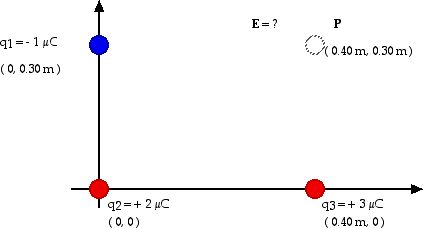
The net electric field is given by
E = E1 + E2 + E3
Be sure that you remember that this is a vector equation!
Now we use Coulomb’s Law to find the individual electric fields E1,
E2, and E3 due to the individual charges
q1, q2, and q3.

E1 = k q1/r12
E1 = (9 x 109 N m2/C2) (1 x 10
- 6 C) / (0.40 m)2
E1 = 5.63 x 104 N/C
This is the magnitude of the electric field. From the diagram, we see
that it points to the left. We can write this specifically as
E1x = - 5.63 x 104 N/C and E1y
= 0
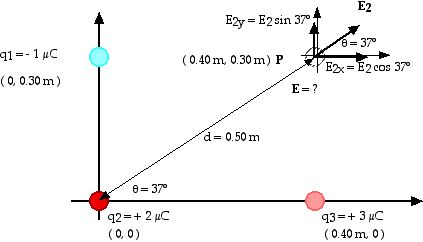
And we continue by calculating E2, the electric field due to charge
q2,
E2 = k q2/r22
E2 = (9 x 109 N m2/C2) (2 x 10
- 6 C) / (0.50 m)2
We found the distance d = 0.50 m from charge q2 to point P by using
the Pythagorean Theorem.
E2 = 7.20 x 104 N/C
Notice the direction from the diagram. E2 = 7.20 x 104
N/C is the magnitude of E2 but we need the components
to specify the direction or to continue with our vector addition problem.
E2x = E2 cos 37° = (0.80) E2
E2x = (0.80)(7.20 x 104 N/C)
E2x = 5.76 x 104 N/C
E2y = E2 sin 37° = (0.60) E2
E2y = (0.60)(7.20 x 104 N/C)
E2y = 4.32 x 104 N/C

E3 = k q3/r32
E3 = (9 x 109 N m2/C2) (3 x 10
- 6 C) / (0.30 m)2
E3 = 3.00 x 105 N/C
E3 = 30.0 x 104 N/C
As before, this is the magnitude and we need to take care of the vector
nature of this by writing
E3x = 0 and E3y = 30.0 x 104
N/C
Now we add (as vectors!) the three electric fields due to the three
charges;
E = E1 + E2 + E3
But this is true only as a vector equation and really means
Ex = E1x + E2x + E3x
and Ey = E1y + E2y + E3y
Ex = (5.63 +5.76+0)x104 N/C and Ey
= (0+4.32+30.0)x104 N/C
Ex = 11.39 x104 N/C and Ey = 34.32x104
N/C
Now that we have the components, we must go back and reconstruct
the net electric field E, finding the magnitude E and the direction  .
.

tan  = opp/adj =34.32/11.39
= 3.01
= opp/adj =34.32/11.39
= 3.01
 = 79.6°
= 79.6°
E = SQRT[Ex2 + Ey2]
E = SQRT[(11.39)2 + (34.32)2] x 104 N/C
E = 36.2 x 104 N/C
Again, I have used SQRT[...] to mean square root of [...] because that is easier
to type.
| Return
to Calendar |
2. Charges q1, q2, and q3 have the
values and locations shown here. What is the electric potential at point P as
shown here?

Of course, this is the same arrangement of charges that we had in the previous
problem. Now, we want to find the electric potential. Remember, electric
potential is a scalar.
The electric potential due to a single point charge q is
V = k q/r
So we begin by finding the electric potential a point P due to each one of
the charges in turn and then add up all these scalar values for the total,
Vtot = V1 + V2 + V3

V1 = k q1/r1
V1 = (9 x 109 N m2/C2) ( - 1 x 10
- 6 C) / (0.40 m)
V1 = - 2.25 x 104 J/C
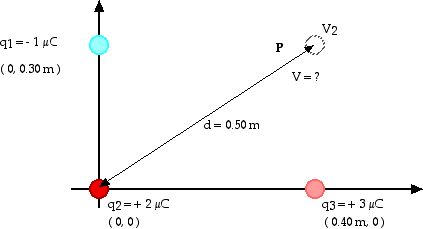
V2 = k q2/r2
V2 = (9 x 109 N m2/C2) ( 2 x 10
- 6 C) / (0.50 m)
V2 = 3.60 x 104 J/C

V3 = k q3/r3
V3 = (9 x 109 N m2/C2) ( 3 x 10
- 6 C) / (0.30 m)
V3 = 9.00 x 104 J/C
Remember, electric potential is a scalar so these electric potentials
add as ordinary numbers,
Vtot = V1 + V2
+ V3
Vtot = ( - 2.25 + 3.60 + 9.00 ) x 104
J/C
Vtot = 10.4 x 104 J/C
Vtot = 10.4 x 104 V
| Return
to Calendar |
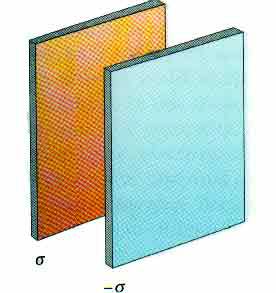
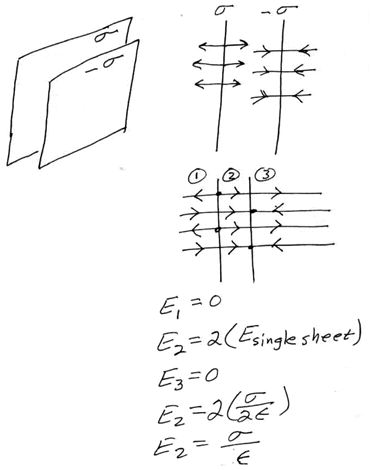
3. (24.58) Two infinite, nonconduciting sheets
of charge are parallel to each other as sketched here. The sheet on the left
has a uniform surface charge density +  ( + sigma
) and the one on the right has a uniform charge density -
( + sigma
) and the one on the right has a uniform charge density -  ( - sigma).
( - sigma).
Show all your work and calculate the value of the electric field
at points
(a) to the left of,
(b) in between, and
(c) to the right of the two sheets.
| Return
to Calendar |
4. The capacitor circuit shown here is connected to a
12-volt power supply.
(a) Calculate the equivalent capacitance of the circuit shown here.
(b) What charge will flow out of the battery?
(c) What charge is stored on the 2.0 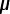 F capacitor?
F capacitor?
(d) What voltage is across the2.0  F capacitor
?
F capacitor
?
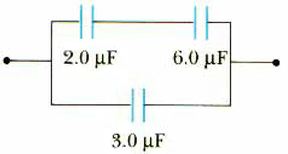
We begin by replacing the 2.0 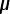 F and
6.0
F and
6.0 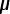 F piece with a single equivalent capacitor of
value Ceq(1).
F piece with a single equivalent capacitor of
value Ceq(1).

1/Ceq(1) = 1/(2.0 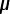 F) + 1/(6.0
F) + 1/(6.0  F)
F)
1/Ceq(1) = [1/2.0 + 1/6.0]/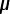 F
F
1/Ceq(1) = [0.5 + 0.1667]/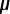 F
F
1/Ceq(1) = 0.6667/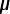 F
F
Ceq(1) = (1/0.6667)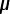 F
F
Ceq(1) = 1.5  F
F
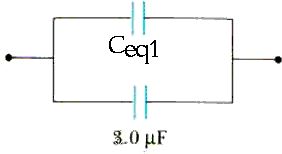
Now, this Ceq(1) = 1.5 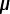 F
capacitor is in parallel with the 3.0
F
capacitor is in parallel with the 3.0 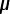 F capacitor
so the single equivalent capacitor that can replace both of these is
F capacitor
so the single equivalent capacitor that can replace both of these is
Ceq(2) = 1.5  F
+ 3.0
F
+ 3.0 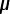 F
F
Ceq(2) = 4.5  F
F
When this equivalent capacitor is connected to a 12-volt power
supply, the charge that flows out of the battery or power supply onto this capacitor
is
C = Q/V
Q = C V
Qtot = (4.5 x 10 - 6 F)(12 V)
Qtot = 5.4 x 10 - 5 C
Where does this charge reall go? Some of it goes onto the 3.0
 F capacitor and some goes onto the earlier equivalent
capacitor Ceq(1). The sum of these two charges is Qtot.
We have enough information to calculate the charge on the 3.0
F capacitor and some goes onto the earlier equivalent
capacitor Ceq(1). The sum of these two charges is Qtot.
We have enough information to calculate the charge on the 3.0  F
capacitor so we begin with that. This 3.0
F
capacitor so we begin with that. This 3.0  F capacitor
has the full 12 volts across it.
F capacitor
has the full 12 volts across it.
Q3 = C3 V3
Q3 = (3.0 x 10 - 6 F)(12 V)
Q3 = 3.6 x 10 - 5 C
Qtot = Q2 + Q3
Q2 = (5.4 - 3.6) x 10 - 5 C
Q2 = 1.8 x 10 - 5 C
Q2 is the charge that flows onto the first equivalent
capacitor Ceq(1) and it is also the charge on the 2.0  F
capacitor (and the same charge is on the 6.0
F
capacitor (and the same charge is on the 6.0 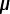 F
capacitor altho’ we do not need that information).
F
capacitor altho’ we do not need that information).
Now for the voltage across this 2.0 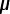 F capacitor.
F capacitor.
C = Q/V
V = Q/C
V2 = Q2/C2
V2 = (1.8 x 10 - 5 C)/(2.0 x 10 - 6 F)
V2 = 9.0 V
V2 = 9.0 volts
And that will mean that
V3 = 3.0 volts
altho’ we do not need that information either.
| Return
to Calendar |
Conceptual Questions:
1. A ballloon is negatively charged by rubbing and then clings to a wall.
Does this mean that the wall is positively charged?
The balloon is attracted to and held in place by charge polarization or charge
induction -- even tho' the wall is electrically neutral. We talked about this
-- and demonstrated it -- in class.
2. Two solid spheres, both of radius R, carry identical total chares,
Q. One sphere is a good conductor while the other is an insulator. If the charge
on the insulating sphere is uniformly distributed throughout its interior volume,
how do the electric fields outside these two spheres compare? Are the fields
identical inside the two spheres?
Outside the radius R, the electric fields are identical.
Inside the radius R, the electric field inside the conductor is zero. Inside
the radius R, the electric field inside the conductor increases linearly with
radius from zero at the center.
3. Give a physical explanation of the fact that the potential energ of
a pair of like charges is positive whereas the potential energy of a pair of
unlike charges is negative.
Think back to the case of gravitational potential energy ( U = m g h ). Suppose
that you choose or define the "reference point" for zero gravitational
potential energy ( U = 0 ) to be on top of a table. If you have a book above
this point it has positive gravitational potential energy and will fall back
to U = 0 if you release it. If you have a book below this point it has negative
gravitational potential energy and you must do work on it to get it back to
U = 0.
Now, look at the electrical equivalent. We have choosen or defined U = 0 to
be the state where the two particles are far, far apart. If we have two like
charges that are near each other, they will go to this state if we release them.
That is, they will repel each other and push each other far, far away. That
means they had positive potential energy when they were nearby. That is not
the case for two unlike charges. If we find them nearby, we must do work on
them to get them to the state we have defined as U = 0. That means they had
negative potential energy when they were nearby.
4. The plates of a capacitor are connected to a battery. What happens
to the charge on the plates if the connecting wires are removed from the battery?
What happens to the charge if the wires are removed from the battery and connected
to each other?
If the wires to the battery are disconnected, the charge remains on the plates
-- and the voltage across the plates remains the same. If the wires are connected
to each other, current will flow and the capacitor will discharge. Then there
will be no voltage across the capacitor nor any charge on the plates.
| Return
to Calendar |


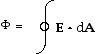
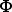 = Q/
= Q/
 /r
/r /2
/2 
 V/
V/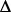 s
s



 .
.
 = opp/adj =34.32/11.39
= 3.01
= opp/adj =34.32/11.39
= 3.01 = 79.6°
= 79.6°



 ( + sigma
) and the one on the right has a uniform charge density -
( + sigma
) and the one on the right has a uniform charge density -  ( - sigma).
( - sigma). 

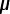 F capacitor?
F capacitor? F capacitor
?
F capacitor
?
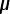 F and
6.0
F and
6.0 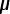 F piece with a single equivalent capacitor of
value Ceq(1).
F piece with a single equivalent capacitor of
value Ceq(1).
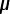 F) + 1/(6.0
F) + 1/(6.0  F)
F)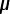 F
F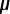 F
F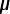 F
F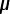 F
F F
F
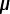 F
capacitor is in parallel with the 3.0
F
capacitor is in parallel with the 3.0 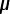 F capacitor
so the single equivalent capacitor that can replace both of these is
F capacitor
so the single equivalent capacitor that can replace both of these is F
+ 3.0
F
+ 3.0 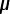 F
F F
F
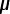 F capacitor and some goes onto the earlier equivalent
capacitor Ceq(1). The sum of these two charges is Qtot.
We have enough information to calculate the charge on the 3.0
F capacitor and some goes onto the earlier equivalent
capacitor Ceq(1). The sum of these two charges is Qtot.
We have enough information to calculate the charge on the 3.0  F
capacitor so we begin with that. This 3.0
F
capacitor so we begin with that. This 3.0 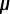 F capacitor
has the full 12 volts across it.
F capacitor
has the full 12 volts across it. F
capacitor (and the same charge is on the 6.0
F
capacitor (and the same charge is on the 6.0 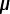 F
capacitor altho’ we do not need that information).
F
capacitor altho’ we do not need that information).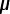 F capacitor.
F capacitor.