Indirect Test of Validity: Two Examples
So far we’ve sketched, in
broad outline, how the indirect argument strategy could be applied to a test of
validity. Now we’ve follow through on
that plan, examining two examples of such an indirect test in detail.
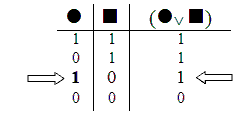
First, consider this little
argument form.
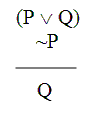
At this point, this little
argument form is an old friend – and one we recognize as clearly valid. We could show directly that this argument
form is valid, by building a truth table for each premise, and for the
conclusion.
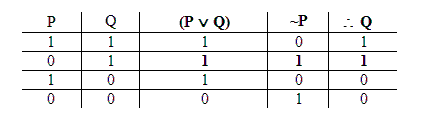
To test the argument indirectly, we do what we always do in an indirect argument: assume the opposite, and then show how that assumption leads to an impossible consequence; since that consequence is impossible (and so false), the assumption of the opposite, which led to that result, must also be false.
Since we’re trying to show that this argument is valid, we assume the opposite by assuming (for the sake of argument) that it’s invalid.
What exactly does it mean to assume that the argument is invalid? Well, if the argument is invalid, then there must be a validity counterexample for that argument. So to assume the argument is invalid amounts to assume that there’s a validity counterexample for the argument: assume there is some possible situation where all the premises of the argument are True, but the conclusion is False.
Summing up: to show indirectly that the argument is valid, we assume the opposite – that is, we assume that the argument is invalid – that is, we assume that there’s a Counterexample – that is, we assume that there’s a possible situation where all the premises are True, but the conclusion is False.
So this is what it looks like to assume the opposite (to assume that the argument is invalid):
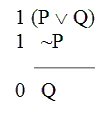
We start our indirect proof of validity by assuming that’s there’s a possible situation like this; and then we chase through all the consequences of this assumption, and try to show how it would lead to an impossible result.
What do we use to “chase through the consequences”? Nothing but our good old semantic rules.
1. Principle of Bivalence:
in any possible situation, a given sentence is either True in that
situation, or else False in that situation. (It can’t be ‘both
True and False’ in that situation.)
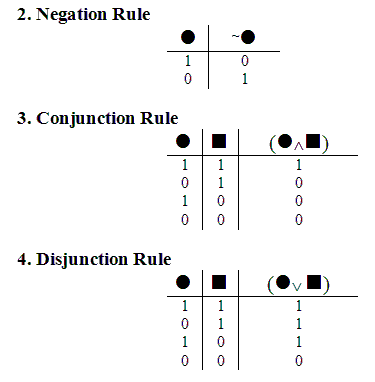
How can our four semantic rules help us chase through the consequences of assuming a validity counterexample?
Notice first that in this situation we’re already committed to the sentence letter “Q” being False.
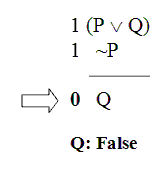
Now, if “Q” is False in this situation, then Bivalence says: you can’t turn around and tell us that “Q” is also True in this situation. No, if “Q” is False in this situation, then it’s False all throughout this situation.
So, since “Q” also shows up in the first premise, we’ve committed ourselves to “Q” being False there as well.
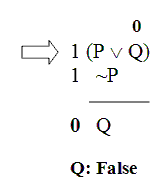
OK, now focus on that first premise. We know two things about that first premise: (i) that its right part, “Q”, is False; and (ii) that the whole sentence is True.
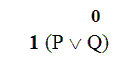
Now, looking at the Disjunction Rule, we see that there’s only one way that you can have the right part of the Disjunction False, but still have the whole disjunction True.
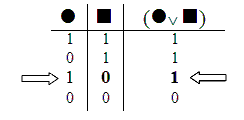
And that’s when the left part is True.
We can apply this point to our first premise to get a new piece of information: since the right part of the disjunction is False, but the whole sentence is still True, we know that the left part must be True.
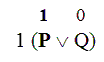
So we’ve chased down one more consequence: we know that in this situation “P” must be True.
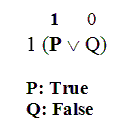
Now we turn our attention to the second premise; this is where the action will take place.
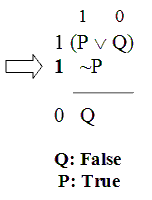
If “~P” is True, then we can use the Negation Rule to work backward to the value of “P”.
The Negation Rule says: if the whole negation is True,
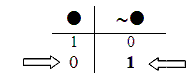
then the original sentence that got negated must be False.
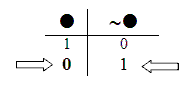
So: since “~P” is True, “P” must be False.
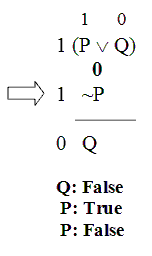
So now we’re committed to “P” being True in this situation, but also False in this situation.
But that’s nuts: no sentence can be True and False in the same possible situation, because that would be a violation of the Principle of Bivalence. Yet that’s where our original assumption led us: by assuming that there is a validity counterexample for this argument, we end up committed to a violation of Bivalence. But a violation of Bivalence is ruled out by our logic. So we see that our original assumption – that the argument is invalid – must also be ruled out by our logic. It must be false that this argument is invalid. This argument must be valid after all.
Let’s review what just happened:
(i) We started out by assuming that the argument is invalid
(by assuming that there is a validity counterexample – a possible
situation where the premises are all True, but the conclusion is False).
(ii) We then used our good old semantic rules to chase through all the consequences of that assumption.
(iii) But the ultimate consequence of that assumption was that we would have a sentence which is True and False at the same time.
(ii) We then used our good old semantic rules to chase through all the consequences of that assumption.
(iii) But the ultimate consequence of that assumption was that we would have a sentence which is True and False at the same time.
But we know from the Principle of Bivalence that that’s impossible. So we know that:
(iv) Our original assumption, that the argument is invalid, leads to a consequence that’s impossible.
So,
(v) Our original assumption, that the argument is invalid, must be false. The argument must have been valid all along.
There you have it: an indirect demonstration that the argument is valid.
Remember the basic steps to what we’ve just done:
(i) Assume that the argument is invalid (by assuming a possible situation where all the premises are True, but the conclusion is False).
(ii) Using the semantic rules to follow through all the consequences of that assumption, show that the assumption would lead to an impossible consequence (namely, a violation of Bivalence – some sentence being True and False at the same time).
(iii) Since Bivalence says it’s impossible for a sentence to be both True and False at the same time, we know that claiming the contrary must be False; and so the original assumption that implies this must have been false as well. So our original assumption – that the argument is invalid – must have been false; the argument must really be valid.
(ii) Using the semantic rules to follow through all the consequences of that assumption, show that the assumption would lead to an impossible consequence (namely, a violation of Bivalence – some sentence being True and False at the same time).
(iii) Since Bivalence says it’s impossible for a sentence to be both True and False at the same time, we know that claiming the contrary must be False; and so the original assumption that implies this must have been false as well. So our original assumption – that the argument is invalid – must have been false; the argument must really be valid.
That’s the basic technique for showing indirectly that an argument is valid. We’ll streamline this technique a great deal, with improved bookkeeping techniques (which we’ll introduce a little later). But already we can understand the basic indirect test.
Next, let’s see what happens if we try this same indirect technique on an argument that really is invalid. What will the end result be then?
Here’s a familiar example.
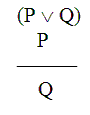
As truth tables show, this argument is invalid: the third valuation is a validity counterexample.

Testing this argument indirectly, we begin by assuming that the argument is invalid – i.e., that there’s a validity counterexample for this argument.
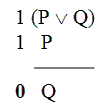
Since the conclusion, “Q,” is False, we’re committed to “Q” being False throughout this situation. And since “Q” shows up in the first premise, we’re committed to it being True there as well.
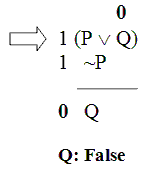
Now, the first premise is a disjunction. And the Disjunction Rule says that if the whole disjunction is True even though its right part is False,
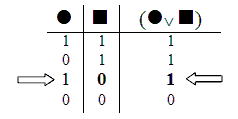
then the left part must be True.
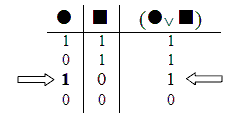
So the left part of the first premise – “P” – must be True.
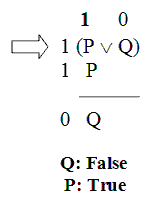
And comparing that to what we said about “P” in the second premise, we see that this is… exactly what we said about “P” all along. Hmm – in this case, even when we followed through all the consequences of our assumption, we didn’t get any nasty violation of Bivalence like we did with the first argument. With this argument everything worked out consistently, and each sentence had only one truth value.
Here it turns out that it’s not at all impossible to have all the premises True, but the conclusion False. Here it turns out that there really is a Validity Counterexample. So here it turns out that the argument really is invalid.
That’s the other half of our indirect test of validity. We already saw the first half: if you assume that the argument is invalid, but that assumption blows up in your face (by violating Bivalence), then the argument was really valid all along. But now we add: if you assume that the argument is invalid, and that assumption doesn’t blow up in your face, then the argument really is invalid.
The first argument turned out Valid according to the Truth Table Test, and also according to the Indirect Test. And likewise the second argument turned out invalid according to the Truth Table Test, and also according to the Indirect Test. That’s not surprising: the two tests will always give the same results, since both of them are applying the exact same semantic rules.
But there is one big difference between the (direct) truth table method, and the indirect method: the number of steps involved.
Consider the first argument we looked at (the valid one), in both the Truth Table and Indirect Tests. Let’s count each sentence we write as one step; and likewise count each “1” or “0” we write as one step. OK, then the truth tables required 4 sentences written across the top, and 4 “1’s” or “0’s” below each of these sentences.
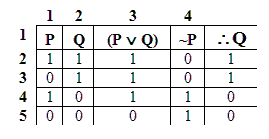
(I didn’t number “Q” on the end, because we already have it listed on the left, next to “P” – I didn’t want to count the same sentence twice.)
The truth table requires 4 x 5 steps – that’s 20 steps.
Now compare that with the indirect method.

Here we had the 3 original sentences, plus 6 0’s and 1’s, for a total of 9 steps.
We see a similar difference when we compare the Truth Table and Indirect test results for the second (invalid) argument. The truth Table Test took 15 steps.

The Indirect Test took 8 steps.
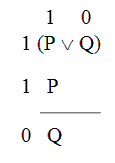
Compare those results:

The Indirect Test gives us an enormous savings in labor. And that’s the main reason we like the Indirect Test so much: because it lets us avoid work. If we weren’t trying to get out of work, we could just stick with the Truth Table test of validity. But since we want to avoid work as much as possible, the Indirect Test is the right one for us.
That’s the first half of our improvements on the original test of validity: do it indirectly, rather than directly (with truth tables). Next, we streamline the indirect test even further – and thereby cut down even further on the amount of work required. How? By getting rid of those annoying “1’s” and “0’s”. And how do we get rid of those? Through improved bookkeeping – the subject of the next lecture.