Introduction to Formal Semantics
Remember our mission: we wanted to develop a new and improved test of validity, a test that didn't rely on sloppy searches for validity counterexamples using just our fuzzy, limited imagination. Our new test of validity would look only at the logical form of the argument – any argument, big or small – and would always tell us if the argument is valid or not.
To pull off that incredible feat, we need to accomplish two tasks:
(i) Get the formNow that we know how to translate from English into our symbolic language – and so managed to extract the logical form of the sentence – we've fulfilled the first of our two requirements. We now know how to get the form of an argument: translate the argument into logical notation, and what we end up with, the final translation, just is the logical form of the argument.
(ii) Test the form.
(Wait, you say: I now know how to extract the logical form of a single sentence; but how do I extract the form of the whole argument? Easy: an argument is, after all, just a string of sentences. Extract the logical form of each of those sentences, and you've extracted the logical form of the whole argument.)
Now that we know how to get the form of an argument, we turn to how we can test the form.
In order to build our wonderful full-proof test of validity – a test that looks only at the freshly-extracted form – we will first build a general semantic theory of our formal language, to match the general grammatical theory we used to build the formal language.
What is a semantic theory, anyway?
Remember the three basic approaches to language that we mentioned earlier in class:
(i) syntax (a.k.a grammar): this studies the form of sentences. (The grammatical rules of our formal language let us test symbolic sentences to make sure they were well-formed sentences.)
(ii) semantics: this studies two (related) features of sentences: their meaning, and their truth/falsehood behavior (when they're true, and when they're false).
(iii) pragmatics: this studies how we use sentences in various different contexts.
We already built a formal grammar for our logical language. (The four clauses of our logical grammar: the basis clause that gave us sentence letters, and the three recursive clauses that gave us negations, conjunctions, and disjunctions.) So we've already covered Syntax. Later on, toward the end of the course, we'll look at Pragmatics. But now we have to turn to the Semantics of our formal language.
Actually, we gave a kind of informal semantics already, when we built our translation techniques. And we did that by approaching our formal language from the meaning end of Semantics. For example, we said that " ~ " means the same as the English word "not".
That's one natural way of explaining the meaning of a foreign word or symbol: translate it into a language we do understand. (Likewise, if I don't understand the meaning of the Hebrew word "yom," you could tell me the meaning by translating it into a language , such as English, which I do understand: it means the same as the English word "day".)
But that was just a rough, incomplete set of translation techniques. Now we want a formal and complete semantic theory, following clear general rules (like our logical grammar), not just sketchy rules of thumb (like our translation techniques).
Notice that I've defined Semantics in a kind of double-barreled way. Semantics deals with both meaning and truth. The two concepts are related, as we saw earlier. (From the rabbit/"Gavagai!" example in class.) We could approach Semantics from either end – starting with meaning, or starting with truth. So which is it going to be?
We're going to build this general semantic theory by starting from the truth-and-falsehood end of Semantics. As we will soon see, we'll get the meaning end too, in the bargain – in fact, we'll fall backward into a formal theory of meaning, without even trying. But we'll start with a theory of when sentences in our formal language are true, and when they're false (what I've been calling the "truth and falsehood behavior" of sentences).
Why start with the truth-and-falsehood end of Semantics? Easy: we're on the path to a formal test of validity: we want to know if an argument is valid, or if instead there's some counterexample making the argument invalid. But think about how we defined "validity" and "validity counterexample":
Valid Argument: an argument where, every time the premises are all true, the conclusion is also trueNotice the central ingredients in these concepts: true and false. We need Truth and Falsehood in order to even talk about Validity, and Validity Counterexamples. And that's why we're building up a theory of Truth and Falsehood for our formal language. (In fact, that's the only reason we're bothering with formal Semantics at all: because we're interested in Validity and Invalidity.) So now we set out building our formal theory of Truth and Falsehood for our formal language.
Validity Counterexample: a possible situation where the premises are all true, but the conclusion is still false.
Keep in mind that we want this semantic theory to be general: it has to handle every single sentence in our logical language, no matter how big or small. No matter what kind of tricky sentence our formal grammar throws at us, the semantic theory must be able to give an account of that sentence's truth and falsehood behavior. Why? Because any sentence might end up being used as a premise or conclusion in an argument; so a general test of validity, one that can handle every argument, will need to be ready for any possible sentence the language can think up.
How can we guarantee that the formal semantics always keeps up with the formal grammar? Well, remember how the formal grammar works: all the sentences in our logical language come from one of the four grammatical rules:
1. Sentence letters are well-formed sentences.
2. Ifis a well-formed sentence, then ~
is a well-formed sentence.
3. Ifand
are well-formed sentences, then (

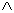
) is a well-formed sentence.
4. Ifand
are well-formed sentences, then (

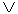
) is a well-formed sentence.
The easiest way of making sure our semantic theory always keeps up with this grammar, is to build a matching rule in the semantic theory for each of these grammatical rules. That way, whichever move the grammar makes – say, building a negation with Clause 2 – the semantics will match that move with its corresponding semantic rule.
That's what we'll do: give a semantic account of each of these four kinds of WFS's. Since altogether they make up all the sentences in our formal language, our semantic account is guaranteed to cover every sentence in the entire language, and be a truly general semantic theory.
There is one fundamental principle that is the foundation for our whole Semantic theory. This is the Principle of Bivalence:
Principle of Bivalence: in any possible situation, a sentence will either be True in that situation, or else it will be false in that situation. (A sentence can't be both True and False in a given situation.)
So, for example, the sentence "Zebras exist" is true in actual situation we're in right now (it's true, in this world of ours, that zebras really do exist). But there could possibly be a zebra-less world, where the sentence "Zebras exist" would be false. That's possible. What isn't possible, according to the Principle of Bivalence, is for there to be a situation where the sentence "Zebras exist" is both true and false at the same time. Likewise, the Principle of Bivalence says there's no possible situation where the sentence "Zebras exist" is neither true nor false. Quite simply, it's always got to be either true or false in a given situation that zebras exist; there's no weird third possibility.
Already, armed only with the Principle of Bivalence, we can state how our formal semantics will handle the simplest kind of WFS – sentence letters.
The Principle of Bivalence says about sentence letters what it says about any sentence: for any given sentence letter, there are only two kinds of possible situations.
(i) the kind of situation where that sentence letter is True, and
(ii) the kind of situation where that sentence letter is False.
So, for example, we know from Bivalence that there are only two kinds of situation as far as the sentence letter "P" is concerned:
(Here I have cleverly used the letter "T" to mark the situation where "P" is true, and the letter "F" to mark the situation where "P" is false.)
If that was too fast, let's practice with another example. Bivalence tells us that there are only two kinds of situation as far as the sentence letter "Q" is concerned:
The answer is four: There's
(i) the kind of situation where both "P" and "Q" are True;and
(ii) the kind of situation where "P is True, but "Q"is False;
(iii) the kind of situation where "P" is False, but"Q"is True;
(iv) the kind of situation where both "P" and "Q" are False.
Of course, we can represent that a lot more easily in the little "T-F" listing used before:
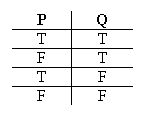
Each of the horizontal lines, of T's and/or F's, depicts a different possible situation.
And what if we consider three different letters, all at the same time – how many different kinds of situations are possible then? Eight:
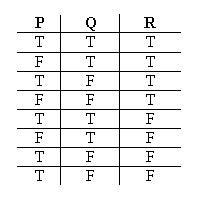
We can see a pattern at work here:

(If you don't know what 2n is, you can go here for a bit of an explanation.)
An easy way to calculate how many different kinds of situations there are, is to put a “2” above each sentence letter, and multiply all the 2's together to get the final, required number. So consider again the little table we built for two sentence letters, "P" and "Q":
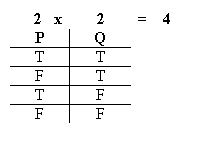
Putting a 2 above each sentence letter, and then multiply together all those 2's, gave us 4
– exactly how many kinds of situations there are, for two sentence letters.
Likewise when we had three sentence letters:
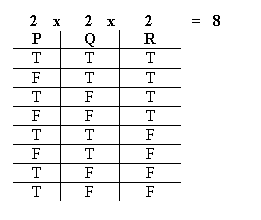
That's right: 3 sentence letters would call for 8 different kinds of situations, to run through every possibility.
(Why does it work out in 2's like that? Because of Bivalence: "P" can go either of 2 different ways – True, or False – and likewise with "Q," and likewise with "R".)
And here's an additional piece of logical jargon: we have a technical name for these different "kinds of situations" – they're called valuations. So we can restate our "number of sentence letters" rule:
for n different sentence letters, we will need 2n different valuations to go through all the different possibilities.
All we've really done with sentence letters is apply the Principle of Bivalence to them (along with some simple combinatorial facts). Of course, the Principle of Bivalence applies to all sentences, not just sentence letters. I've been focusing on Bivalence for sentence letters, and how many different valuations we need to go through all the possibilities, because honestly that's all I have to say about sentence letters. Sentence letters are pretty simple, in terms of logical grammar: they're just little atoms, with no moving parts. And it turns out sentence letters are just as simple semantically: they're either true or false, and that's about it.