1. Chain Arguments. Consider this passage:
Jack is a short-haired cat, so he’s
not a Birman. But he can’t be a tabby,
since he has seal-point markings.
Therefore Jack is either a Siamese or a Burmese.
It seems fairly clear that this is an argument. And if it’s an argument, then it has a conclusion, the claim that it’s arguing for. What is the conclusion of this argument?
That looks clear as well: the last sentence – “Jack is
either a Siamese or a Burmese” – (i) is preceded by the conclusion marker
“therefore”, and moreover (ii) comes in a natural place for a conclusion
(namely, at or near the end of the passage).
So we might think the official, cleaned-up form of the argument would be
like this:

But take a closer look at that first sentence:
Jack is a short-haired cat, so he’s not a Birman.
The conclusion marker “so” in the middle makes clear that this is in fact a combo sentence – a little miniature argument all on its own, with a premise and a conclusion. Since “so” comes right before “He’s not a Birman,” that’s the conclusion of this miniature argument. In official form, this little combo-sentence would break apart like this:
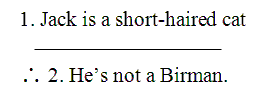
In fact, the second sentence is also a combo sentence.
He can’t be a tabby, since he has seal-point markings
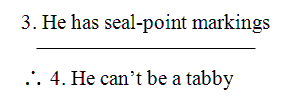
What we see in this example – thanks to the two combo sentences – is the possibility of an argument containing smaller arguments as parts.

Sentences (1) and (3) are clearly premises; and sentence (5)
is clearly a conclusion. But what are
sentences (2) and (4)? Each is a conclusion,
following from a previous sentence. But
(2) and (4) also act as premises. They provide evidence in support of
the final conclusion, (5): it’s because Jack is neither a Birman, nor a
tabby, that we conclude that he must be either a Siamese or a Burmese.
Sentences (2) and (4) are hybrid sentences, acting as
both premises and conclusion. We
will call such a sentence a sub-conclusion: a conclusion that
turns around and acts as a premise in support of a further
conclusion. (Likewise we will say that
the little argument that a sub-conclusion is the conclusion of, is a sub-argument. The argument from (1) to (2) is a
sub-argument; and the argument from (3) to (4) is also a sub-argument.)
Because a sentence can be a hybrid-like sub-conclusion in
this way, we are able to link together a number of arguments, into one long chain
argument. The whole big argument,
from (1) to (5), is a chain argument, with two sub-arguments as parts. We will say that the final conclusion of the
argument – sentence (5) – is the main conclusion of the whole
argument. It’s the main conclusion
in this passage, because it’s the only conclusion that doesn’t turn
around and support some further conclusion. The main conclusion is the end of the line in
a chain argument.
2. Argument Diagrams. Once we realize that an argument can be a chain argument, we see what was wrong with our first stab at putting this argument into official form.


This listing of sentences does show the argument’s official form. The problem with writing an argument’s official form in this ‘stacked up’ sort of list, however, is that such a list will get complicated pretty quickly when we turn to bigger chain arguments. For instance, if there were three sub-conclusions supporting the main conclusion, we’ll need to depict three vertical columns of sentence lists. And if there were further sub-arguments above those, the whole array would spread out into even further vertical columns. That could become a complicated, hard-to-read mess.
But once we’ve numbered each sentence, we can instead represent the structure of the argument by building an argument diagram. In an argument diagram, we show that one sentence is supporting another sentence by drawing an arrow from the first sentence (the premise) to the second (the conclusion).

If more than one premise is supporting the same conclusion, we use a “+” sign to link the premises, as well as the arrow pointing down to the conclusion.

In the argument we’ve been looking at, the first sentence is a premise in support of the second.

Likewise, the third sentence is a premise in support of the fourth.

And sentences (2) and (4) are meant to support the main conclusion, sentence (5).
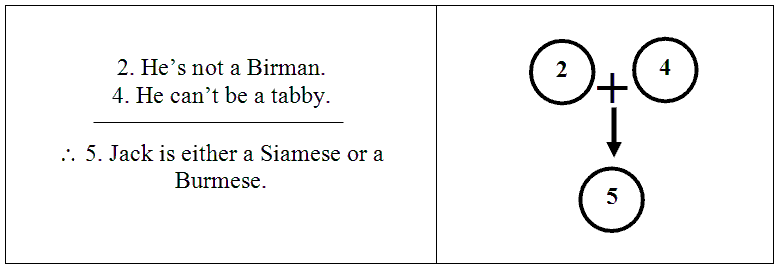
Putting all of these links together, we get a diagram for the entire argument.
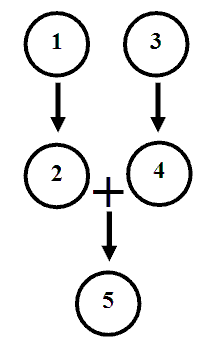
Argument diagrams provide a very clear, compact way of representing the official form of chain arguments. As we turn to more and more complex chain arguments, argument diagrams will allow us to continue showing which sentences in an argument are meant to support which, without the messy sprawl involved in writing out each premise above the conclusion it supports. So from now on, we can represent the official form of an argument by first numbering each sentence, and then constructing an argument diagram.
Of course, when numbering, we need to give each sentence a different number from all the other sentences. In particular, we need to break each combo sentence into its two smaller sentences, and give those two smaller sentences different numbers. Once that numbering is in place, however, we don’t need to write out those sentences all over again in order to show the argument’s official form. Instead, we can just put the sentence numbers into an argument diagram.