PHY1161G
Exam #3

November 1, 2000

Possibly useful information:
For reflection, _inc = _ref

For refraction, n₁ sin ₁ = n₂ sin ₂
n = c/v

image equation
apparent depth d_i = d_o (n₁/n₂)
Young’s Double Slit: = d sin

d sin = m , maxima for m = 0, 1, 2, . . .
d sin = (m + ¹/₂) , minima for m = 0, 1, 2, . . .

diffraction grating: = d sin
d sin q = m l maxima for m = 0, 1, 2, . . .
diffraction by a slit: D = D sin
First minimum for D = D sin =
sin = / D
/ D
Minima for D = D sin = m , m = 1, 2, 3, . . .
optical resolution: 1.22( / D )
polarization: S = S_o cos²
thin films: ’ = / n
2t = m ’ = m( / n); max, m = 0, 1, 2, . . . n₁ < n₂ < n₃
2t = (m+¹/₂) ’ = (m+¹/₂)( / n);
min, m = 0, 1, 2, . . . n₁ < n₂ < n₃
2t = m ’ = m( / n); min, m = 0, 1, 2, . . . n₁ < n₂ > n₃
2t = (m+¹/₂) ’ = (m+¹/₂)(l / n);
max, m = 0, 1, 2, . . . n₁ < n₂ > n₃
Simple Magnifier: M_ang = ^r / _f = ^{25 cm} / _f
Microscope:
Telescope:
We have covered lots of good things in this section! There may, indeed, be too many questions. So budget your time wisely.

Statistics:

High: 96

Mean: 65

Low: 18 (then 29)

We begin with Snell’s law,

n₁ sin ₁ = n₂ sin ₂
(1.33)(sin 30°) = (1.00) sin ₂
(1.33)(0.5) = (1.00) sin ₂
sin ₂ = 0.665

₂ = 41.7°

The intensity is given by

S = S_o cos²

[This is contained in the text, on page 885, before Example 23.8; the equation given in Example 23.8, at the top of page 886, is NOT correct].

S = S_o cos²
S = S_o cos² = S_o/2
cos² = 0.50
cos = 0.707
= 45°

b) Consider two parallel polarizing filters, A and B, as shown below. Another polarizing filter, C, is placed between them. As this third polarizing filter C is rotated through a full 360°, how many times does the beam of light cycle from dark to bright?

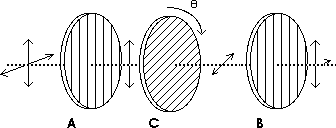
The light coming from a polarizer is always aligned with the direction of the polarizer.

If polarizer C is perpendicular to polarizer A, no light will get through. If polarizer C is perpendicular to polarizer B, no light will get through. But polarizers A and B are parallel. Therefore, polarizer C will be perpendicular to both A and B twice as it is rotated through 360^o.


c) Consider two perpendicular polarizing filters, A and B, as shown below. Another polarizing filter, C, is placed between them. As this third polarizing filter C is rotated through a full 360°, how many times does the beam of light cycle from dark to bright?

The light coming from a polarizer is always aligned with the direction of the polarizer.

If polarizer C is perpendicular to polarizer A, no light will get through. If polarizer C is perpendicular to polarizer B, no light will get through. Polarizers A and B are perpendicular. Therefore, polarizer C will be perpendicular to either A or B four times as it is rotated through 360^o.

Locate the image.
Describe the image:

Always start with a clear ray diagram; this is more useful to understanding than just solving the equation. Always ask if the solution to the equation is consistent with your ray diagram.

Now we are ready for the image equation,

The focal length is one-half the radius of curvature

Your face is the object so the object distance is d_o = 25 cm

1 / d_i = .01667 - .04
1 / d_i = - 0.02333
d_i = 1 / ( - 0.2333)
d_i = - 43.9 cm

The negative sign means this is a virtual image.

We can find the magnification from

M = - [ ( - 43.0 cm ) / 25 cm ]
M = 1.76

The magnification is M = 1.76. This positive magnification means the image is upright. Since M > 1, the image is enlarged.

4. Consider an object placed 30 cm from a converging lens with a focal length of 10 cm.
Locate and characterize the image:
Where is the image located?
Is the image real/virtual; upright/upside-down; smaller/larger?

From the ray diagram, we can see that the image is real, inverted, and smaller.
Now, let’s do the numerical calculation:

Now, the magnification: M = - [ ^di / d_o ]

The image is inverted and one-half the height of the object.

5. A HeNe laser ( = 634 nm) shines light onto a double slit with slit separation distance of d = 0.2 mm. An interference pattern of dark and bright areas is produced on a screen 2 m from the double slit. What is the distance between the bright central maximum and the first dark area on either side of it?

A maximum occurs for

d sin = m

But we need the angle for a minimum.
Minima occur for

d sin = (m + ¹/₂)

This first minimum is for m = 0, so

d sin = (¹/₂)
(0.2 mm) sin = (0.5)( 634 nm )
( 0.2 x 10 ^{- 3} m) sin = (0.5)( 634 x 10 ^{- 9} m )
sin = ( 0.5)( 634 x 10 ^{- 9} m ) / (0.2 x 10 ^{- 3} m)
sin = ( 0.5)( 634 x 10 ^{- 9} ) / (0.2 x 10 ^{- 3} )
sin = 1.585 x 10 ^{- 3}
= 0.0908^o
tan = 1.585 x 10 ^{- 3}
tan = ^y/_L
y = L tan
y = ( 2.00 m) ( 1.585 x 10 ^{- 3} )
y = 3.17 x 10 ^{- 3} m
y = 3.17 mm

---

6. As in the lecture demonstration, a light source consists of a long, thin tube or filament. A meter stick is placed very near the light source. At a distance of L = 2.0 m, there is a diffraction grating with 750 lines / mm.
a) What is the separation distance d between the lines in the grating?

When you look at the light source, where -- how far from the light source, along the meter stick -- will you see the spectrum spread out?
b) At what position will you see red light with = 700 nm?
c) At what position will you see violet light with  = 400 nm?

First, the diffraction line separation,

Units are important! Don't forget to carefully consider and include units!

Light will be bent by the diffraction grating at angles that correspond to the wavelengths according to

d sin = m

We are concerned only with the first-order spectrum, so m = 1 and

d sin =

d sin =
sin = /_d

For red light,

= 700 nm = 700 x 10 ^{- 9}m
sin = (700 x 10 ^{- 9}m) / (1.33 x 10 ^{- 6} m)
sin = (700 x 10 ^{- 9}) / (1.33 x 10 ^{- 6})
sin = 0.526
= 31.7^o
tan = 0.619
tan = ^y/_L
y = L tan
y = ( 2.00 m) (0.619)
y = 1.23 m = 123 cm


d sin =
sin = /_d

For violet light,

= 400 nm = 400 x 10 ^{- 9} m
sin = (400 x 10 ^{- 9}m) / (1.33 x 10 ^{- 6} m)
sin = (400 x 10 ^{- 9}) / (1.33 x 10 ^{- 6})
sin = 0.301
= 17.5^o
tan = 0.315
tan = ^y/_L
y = L tan
y = ( 2.00 m) (0.315)
y = 0.631 m = 63.1 cm