PHY1161C
 Key #4
December 6, 2000

| Return to 1161 Calendar |

Possibly useful information:
c = 3.00 x 108 m/s h = 6.626 x 10-34 Js = 4.14 x 10-15 eV s



E = m c2 E = h f
KEmax = h f - Wo = h/p = h / mv
(x) (px) Å h for SHO, Eo = h f / 2
R = 1.097 x 107 m - 1 E = Ei - Ef = h f
,


Subshells: l = 0, 1, 2, 3, . . .; s, p, d, f, g, h, . . .

1 u = 931 MeV/c2
u
Mev/c2
kg
electron
0.00054858
0.511
9.1094 x 10 - 31
proton
1.007276
938.27
1.67262 x 10 - 27
neutron
1.008665
939.57
1.67493 x 10 - 27
hydrogen
1.007 825

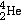
---> + Q = ( mP - mD - ma) c2
 --- > + b- + Q = ( mP - mD ) c2
--- > + b+ + n Q = ( mP - mD - 2 mb ) c2
N = No e - t T1/2 = 0.693/
| Return to 1161 Calendar |

1. [25 pts] (similar to 27.2) A flashbulb goes off at the origins as the origins of our usual reference frames A and B coincide. Frames A and B have a relative speed of 0.8 c along their x-axes. A wavefront travels along the x-axis as observed in B.
a) [ 6 pts] What time is recorded in B as this wavefront reaches xB = 1,000 m?
b) {14 pts] Use these values of xB and tB to calculate the coordinates xA and tA that describe this event in A.
c) { 5 pts] Then use these values to calculate the speed of light in reference frame A ( vlight = xA/tA).


To find time tB we just use the definition of velocity

v = c = xB/tB
tB = xB/c


tB = 3.333 x 10 - 6 s

Of course, we also have

xB = 1000 m

 


Now we can apply the Lorentz Transformations to find xA and tA,






xA = 3 000 m





tA = 1.0 x 10 - 5 s

Now we can find the velocity in the A-frame and determine if the Lorentz Transformations work. Is it, indeed, true that the velocity of light will be the same in both frames? Let’s see, . . .



vA = 3.00 x 108 m/s

And, indeed, this is the speed of light!

2. [15 pts] (similar to 27.49) A spaceship travels away from Earth at a velocity of 2.5 x 108 m/s. A projectile is shot forward from the spaceship at 1.5 x 108 m/s relative to the spaceship. What is the velocity of the projectile relative to Earth?


This provides a more direct application of our velocity transformation equation,

with

v = 2.5 x 108 m/s
vxCB = 1.5 x 108 m/s





vxCA = 2.82 x 10 8 m/s

3. [10 pts] (28.15) What is the energy of the photons in the visible region of the electromagnetic spectrum? (Use = 550 nm as an average value)?

E = h f
f = c
f = c /
E = h c /
E = (4.14 x 10-15 eV s) (3.0 x 108 m/s) / 550 nm
E = (4.14 x 10-15 eV s) (3.0 x 108 m/s) / 550 x 10 - 9 m
E = 2.26 eV

4. [15 pts] (28.41) What is the wavelength of an electron moving at 1.5 x 108 m/s (v = 0.5 c)?

= h/p = h / mv
= (6.626 x 10-34 J s) / [(9.11 x 10 - 31 kg)(1.5 x 108  m/s)]
= 4.85 x 10 -12 m

This wavelength is larger about a nuclear diameter and is a reasonable fraction of typical atomic spacing.

5. [15 pts] (29.1) Calculate the first wavelength of the Balmer series for hydrogen and tell what color it is.
Balmer Series for Hydrogen:


R = 1.097 x 107 m -1, Rydberg constant

For n = 3 we have


= (1.097 x 107 m-1) (0.1389)
= 1.525 x 106 m-1
n=3 = 6.563 x 10-7 m
n=3 = 656.3 x 10-9 m
n=3 = 656.3 nm

and this is red light

6. [20 pts] (29.16) In state “A” the energy of an atom is - 3.45 eV and in state “B” its energy is - 5.67 eV.
a) [7 pts] What is the energy of the photon emitted in the transition from “A” to “B”?
b) [7 pts] What is the wavelength of this photon?
c) [6 pts] What color is the light of this photon?

Ephoton = E = EA - EB
Ephoton = (- 3.45 eV) - (- 5.67 eV)
Ephoton = 2.22 eV

E = hf = h(c/)
= hc/E
= (6.626 x 10 - 34 Js)(3.0 x 10 8 m/s) / 2.22 eV

We need to convert E = 2.22 eV into units of J (or the equivalent) to finish carrying out this calculation


E = 3.55 x 10-19 J
= (6.626 x 10 - 34 Js)(3.0 x 10 8 m/s) / 3.55 x 10 - 19 J
= 5.60 x 10 - 7 m
= 560 x 10 - 9 m = 560 nm

This is yellow light, near the middle of the range of visible light.

| Return to 1161 Calendar |

(C) 2002, Doug Davis; all rights reserved