Hour Exam 2
October 17, 2001
Return to PHY 1350's Home Page
PHY 1351
Hour Exam 2
October 17, 2001
Return to PHY 1350's Home Page
Conceptual Questions:
1. Q6.4 Why does mud fly off a rapidly turning automobile tire?
For mud to move in a circle, there must be a (net) force on it -- directed toward the center of the circle. The value of that force is Fc = m v2/ r. As the velocity (or speed) increases, that force must increase if the piece of mud is to continue to move in a circle. As the velocity increases, the force that holds the mud to the wheel reaches its limit and the mud can no longer go around in a circle. When that limit is reached, the mud separates from the tire.
2. Q6.8 Describe a situation in which a car driver can have a centripetal acceleration
but no tangential acceleration.
Uniform Circular Motion (UCM) is just such a situation. There will always be a centripetal acceleration in circular motion because of the changing direction. If the motion is uniform -- if the speed is constant -- there will be no tangential acceleration.
3. Q7.4 Can the kinetic energy of an object be negative?
No. Kinetic energy is given by KE = (1/2) m v2. The mass m is always positive and v2 is positive so KE must always be positive (of course, if v = 0 then KE = 0). KE can not be negative.
4. Q7.14 An older model car accelerates from 0 to a speed v in 10 s. A newer,
more powerful sports car accelerates from 0 to 2 v in the same time period.
What is the ratio of powers expended by the two cars?
Assume the two cars have the same mass.
The car going 2 v has four times the Kinetic Energy. If it acquired this much energy in the same time, then the power supplied to it is also four times as much.
5. Q8.10 What would the curve of U versus x look like if a particle were in
a region of neutral equilibrium?
Neutral equilibrium means zero net force. The force is the slope of the U vs x curve. That means the slope is zero so the curve is a straight, horizontal line.
1. (6.63) An amusement park ride consists of a large vertical cylinder that
spins about its axis fast enough that any person inside is held up against the
wall when the floor drops away. The coefficient of static friction between the
person and the wall is µs, and the radius of the cylinder is
R.
Show that the maximum period of revolution necessary to keep the person from
falling is T = (4 
2
R µs /g)1/2 or T = SQRT(4 2
R µs /g) .
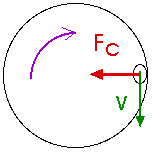
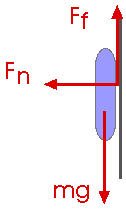
Fx = - Fn
= - m v2 / R = - Fc
Fn = m v2 / R
Fy = Ff -
m g = 0 = m ay
Ff = m g
Ff = 
Fn
Ff = Fn = ( m v2 / R)
= m g
( m v2 / R)
= m g
v = C / T = 2 
R / T
v2 = 4 2 R2
/ T2
( [4 2 R2
/ T2] / R) = g
T2 = 4 2 R / g
T = [ 4 2 R / g ]1/2
2. (6.21) A roller-coaster vehicle is on the track shown below.
(a) What is the maximum speed the vehicle can have at B and still remain on
the track?
(b) What must be the vehicle’s speed at point A to reach point B with the
speed you just calculated?
To "still remain on the track" means the normal force Fn has just gone to zero, Fn = 0.
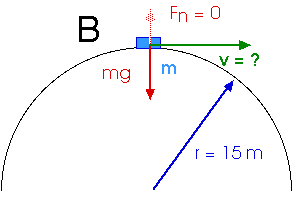
With the normal force equal to zero, there is only the weight mg available to supply the centripetal force Fc,
Fc = Fnet
m v2 / r = m g
v2 / r = g
v2 = g r = (9.8 m / s2 ) (15 m) = 147 m2/s2
v = 12.12 m /s
(b) What must be the vehicle’s speed at point A to reach point B with the speed you just calculated?
EA = EB
KA + UA = KB + UB
( 1/2 ) M vA2 + 0 = ( 1/2 ) M (12.12 m/s)2 + M (9.8 m/s2) (20.0 m)
( 1/2 ) vA2 = ( 1/2 ) (12.12 m/s)2 + (9.8 m/s2) (20.0 m)
( 1/2 ) vA2 = ( 1/2 ) (147 m2/s2 ) + ( 196 m2/s2 )
( 1/2 ) vA2 = ( 73.5 m2/s2 ) + ( 196 m2/s2 )
( 1/2 ) vA2 = ( 269.5 m2/s2 )
vA2 = 539 m2/s2
vA = 23.2 m/s
3. (4 ed; 7.4) A block of mass 0.60 kg slides 6.0 m down a frictionless
ramp inclined at 20o to the horizontal. It then travels on a rough horizontal
surface where 
k = 0.50.
(a) What is the speed of the block at the end of the incline?
(b) What is its speed after traveling 1.00 m on the rough surface?
(c) What distance does it travel on this horizontal surface before stopping?
On the frictionless incline, the normal force does no work, Wn= 0. Only the force of gravity does any work,Wg = F s cos
= ( m g ) (6.0 m) cos 70o = (0.60 kg) (9.8 m/s2) (6.0 m) (0.342) = Wg = 12.1 J
Notice that this has the cosine of 70o rather than of 20o. In writing W = F s cos
Wnet = Wg + Wn = 12.1 J
Wnet =
KE = KE - KEi = KE
Wnet = (1/2) m v2
(1/2) m v2 = (1/2) (0.60 kg) v2 = 12.1 J
v2 = 40.22 m2 / s2
v = 6.34 m / s
This is the speed at the bottom of the incline and the beginning of the rough horizontal plane that has friction.
From the force diagram, you can see that
Fn = m g = (0.60 kg) (9.8 m/s2) = 5.88 N
Ff =
Along this rough, horizontal plane, only this friction force Ff does any work. By the time the block has moved a distance of 1.0 m along the plane, the net work done on the block is
Wnet= Wf = - (2.94 N) (1 m) = - 2.94 J
Wnet =
KE1.0 m = 12.1 J - 2.9 J = 9.2 J
KE1.0 m = 9.2 J = (1/2) m v2 = (1/2) (0.60 kg) v2
v2 = 30.7 m2 / s2
v = 5.5 m / s
Now, how far does it travel before it completely stops? At that point, KEf = 0. The work done by friction in moving this distance X is
Wnet= Wf = - (2.94 N) ( Xf )
And this is just equal to the change in KE, from its initial value of 12.1 J at the bottom of the inclined plane until it goes to zero,
- (2.94 N) Xf = - 12.1 J
Xf = 4.11 m
We will measure the gravitational potential energy Ug from the "final" position of the 5.0-kg mass.
Ei = 0 + m2 g h2
Ei = 0 + (5.0 kg) (9.8 m/s2) (2.0 m)
Ei = 98.0 J
This amount of energy goes into the kinetic energy of the system -- the kinetic energy of both masses -- and the heat associated with the work due to friction.
Kf = (1/2) (8 kg) v2 = (4 kg) v2
Uf = 0
Ef = Ei + Wf
Wf = - Ffs
Ff =
Fn
Fn = m1 g
Fn = (3.0 kg) (9.8 m/s2)
Fn =29.4 N
Ff = (0.30) (29.4 N) = 8.82 N
Wf = - (8.82 N) (2.0 m)
Wf = - 17.6 J
Ef = 98.0 J - 17.6 J = 80.4 J
Ef = Kf = (1/2)(m1 + m2) v2 = (1/2) (3 kg + 5 kg) v2
Ef = Kf =(4 kg) v2 = 80.4 J
v2= 20.1 m2/s2
v = 4.5 m/s
Return to PHY 1350's Home Page
