|
|

|
|


We see ourselves in the mirror every morning. How does a mirror
work? Figure 18.2 shows light originating from a point and striking
a mirror. That point is labeled O and we call it the object; this
is where the object really is and where the light originates.
Each ray is reflected according to the law of reflection, that
the angle of reflection (r) equals the angle of incidence (i);
this is indicated for one ray but it is true for every ray. After
reflecting from the mirror, these rays diverge as if they had
originated from the single point behind the mirror that is labeled
I. This is the image. In this case it is called
a virtual image; the light does not pass through
the image but only appears to be coming from it. A plane mirror
produces a virtual image behind the mirror. Dotted lines in the
figure are extensions of the outgoing rays; they show where the
rays look as though they had come from. Our eyes see light that
looks like it came from this point; that is what we mean by the
image.



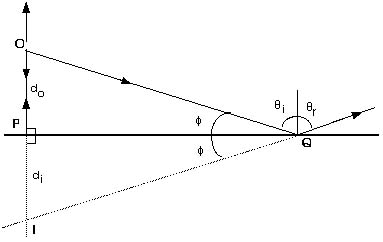
But we can be more specific. Figure 18.3 shows just two rays from
the many rays of Figure 18.2. Ray OP leaves the object normal
to the mirror, strikes the mirror, and is reflected back upon
itself. It could have come from anywhere along the line IP. Ray
OQ leaves the object and strikes the mirror at point Q where it
is reflected according to the law of reflection. After leaving
the mirror it looks like it originated somewhere along line IQ.
Of course point I is the only place consistent with both these
rays. Q is any point at all so I is the image; the light looks
like it came from point I. In Figure 18.3 there are two identical
right triangles. Angles OPQ and IPQ are both right angles. Angle
f is the same for both. And length PQ is certainly the same for
both. Therefore side OP equals side IP. These have also been labeled
do for object distance and di for image
distance. Thus, the virtual image produced by a plane mirror is
just as far behind the mirror as the object is in front of the
mirror. This is true for every point on the object and image.
That means the image will be exactly the same size as the object
(we could say it has a magnification of 1.00). The
image is also right-side-up or erect. The image in a mirror undergoes
a right-left reversal; when you wave at your image with your right
hand the wave is returned by the left hand of your image.


It is fun to look at the images produced by multiple reflections.
Figure 18.4 shows two mirrors set perpendicular to each other.
An object is placed at point O. Image I1 is produced
by a single reflection from mirror #1 and image I2
is produced by a single reflection from mirror #2. But there is
still another image, I12 produced by two reflections,
from both mirror #1 and #2. You can think of this as the image
in mirror #2 of image I1 or the image in mirror #1
of image I2. Each reflection reverses the image from
right to left. So image I12 is not reversed at all.
Wave at yourself in such a corner mirror and see which hand waves
back! Or hold up your Adventures in Physics book
in front of such a corner mirror and read its title!

Q: How many images are produced by two mirrors placed at 60 to each other?
A: Symmetry is an important aspect of Physics. Symmetry will often allow an easy solution to an otherwise difficult problem. Instead of looking at all the individual rays and their reflections, we will apply symmetry to this problem.
Object O is place between Mirror #1 and Mirror #2. Rays that undergo
a single reflection on Mirror #1 produce image I1;
a single reflection from Mirror #2, image I2. Mirror
#1 produces an image of Mirror #2; this is labeled M12.
There is an image in that mirror, I12. That image is
the result of two reflections--from Mirror #1 and then Mirror
#2. Likewise, image I21 is also the result of two reflections
from Mirror #2 and then Mirror #1. Three reflections are also
possible and produce one more image, labeled I121 or
I212. This is the principle of a Kaleidoscope. Each
point on the object appears as five images for a total of six
things to look at!



|
|