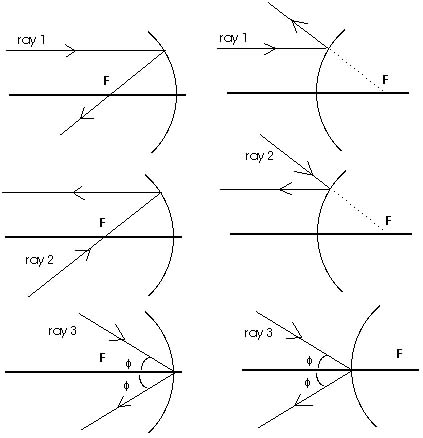
Figure 18.8 shows an object placed some distance from a concave mirror. We have used an arrow for convenience. The tail of the arrow is on the optic axis. Simply from symmetry, we know that the image of this tail must also lie somewhere on the optic axis; whatever argument you can think of for the image's being above the axis is just as valid for its being below the axis. Therefore, all we need to do is to locate the image of the tip of the arrow. We can then draw in the rest of it just by dropping a line to the axis. While an infinite number of rays leave the tip of the arrow (or any other point on the arrow), we will concentrate on just the three principal rays shown in the first part of the figure. Having an image means that all of the rays that leave the object and are reflected from the mirror will pass through a single point that locates the image. If we construct a ray diagram using just two rays and find that they intersect we have determined the location of the image. However, it is prudent to confirm this with a third ray. If you draw three rays and they do not intersect at a single, common point then you know an error has occurred and you can track it down or begin again. Notice that the real image is inverted.

Figure 18.8 shows a real image produced. For a real image, the reflected light actually passes through the image. If a card or screen is placed at the location of the image an image will be projected on the card or screen. But a mirror can also produce a virtual image. Figure 18.9 shows additional examples of real images being produced by a concave mirror when the object is placed at various distances from the mirror. A far distant object produces a small, inverted, real image when reflected in a concave or converging mirror. Bringing the image in closer to the mirror enlarges the size of the image. When the object is at a distance of twice the focal length from the mirror, the image is the same size as the object (and still inverted). Moving the object in even closer makes the image larger than the object.

The magnification of a situation is the ratio of the image height to the object height. If the image is inverted, we will consider the image height negative so the magnification will be negative. If Figure 18.9, when the object is far away, the image is smaller in size and is upside down so the magnification is small and negative, like M = - 0.75 or M = - 0.50. When the object distance is two times the focal length, the image is the same size as the object and is upside down so the magnification is M = - 1.00. As the object moves closer than this, the image increases in size but remains upside down so the absolute value of the magnification continues to increase although the magnification is still negative.

Figure 18.10 shows two examples of producing a virtual image by a mirror. One is by a concave or converging mirror; the other, a convex or diverging mirror. Concave mirrors can produce either real or virtual images from a real object depending upon where the object is. If the object is beyond the focal point the mirror will produce a real image; if inside the focal point (between the mirror and the focal point), a virtual image. Convex mirrors produce only virtual images from real objects. A virtual image is very "real" in that you can see it quite clearly. But it can not be projected. If you place a card behind the mirror at the location of the image, there will be nothing projected upon it. Think again of your own virtual image in the bathroom mirror this morning. If you had held a card behind the mirror you would not have found your image projected upon it. While a virtual image can easily be seen, the light does not actually pass through the location of the image. That is precisely what is meant by a virtual image.

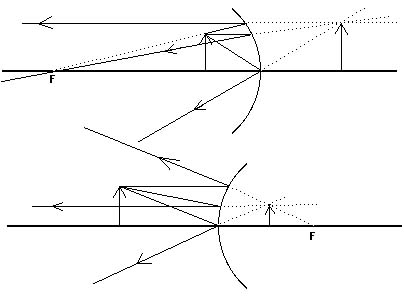
Virtual images due to a reflection in a mirror will be right side up so the magnification will be positive in these cases. In Figure 18.10, the magnification is greater than one (M > 1.00) for the enlarged virtual image due to the concave mirror. The magnification is less than one (M < 1.00) for the reduced virtual image due to the convex mirror.

Ray diagrams are essential in understanding image formation. If they are carefully constructed all the dimensions can be accurately measured.

Q: What kind of images can a concave mirror produce?

A: Depending upon the distance the object is from the mirror, a concave mirror can produce a real or virtual image and the image can be enlarged or reduced in size. A shaving mirror or a make-up mirror is a good example of a concave mirror. The inside of a shiney spoon is another example of a concave mirror.

Q: What kind of images can a convex mirror produce?

A: For a real object, a convex mirror will always produce a virtual image that is reduced in size. The passenger-side rearview mirror on a car is a good example of a convex mirror. The outside of a shiney spoon is another example of a convex mirror.