Homework

Chapter 5; Newton's Third Law of Motion

Homework: Ex 6, 8, 11, 12, 13, 14, 17, 19, 23, 24, 25, 28, 32; Pb 1, 2, 3, 6

Ex 5.6 When you drop a rubber ball on the floor it bounces almost to its original height. What causes the ball to bounce?

The floor exerts an upward force on the ball -- that stops the ball and gives it an acceleration upward.

This upward force from the floor will cause the ball to deform or change shape while it is in contact with the floor.

Ex 5.8 Two 100-N weights are attached to a spring scale as shown. Does the scale read zero, 100 N, or 200 N -- or some other reading?

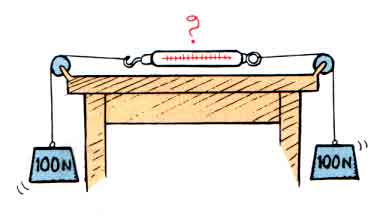
The scale reads the tension in the string. The tension in the string is 100 N. This is the force the string must exert up on either of the 100-N weights at either end of the string.

Nothing is moving, nothing is accelerating, so the net force on the spring is zero. Likewise, the net force on either of the 100-N weights is also zero. But that is another question. The spring scale does not measure the net force. The spring scale simply measures the tension, the magnitude of the force exerted by the string.

Ex 5.11 Why can you exert greater force on the pedals of a bicycle if you pull up on the handlebars?

The handlebars then pull down on you, somewhat as if someone were pushing down on your shoulders. This lets you exert a greater downward force on the pedals

Ex 5.12 Does a baseball bat slow down when it hits a ball?

Of course. When the bat exerts a force on the baseball, the baseball also exerts a force on the bat -- in the opposite direction.

Ex 5.13 Why does a rope climber pull downward on the rope to move upward?

As the climber pulls down on the rope, the rope pulls up on the climber. This is another good example of Newton's Third Law or the Law of Action and Reaction.

Ex 5.14 You push a heavy car by hand. The car, in turn, pushes back with an opposite but equal force on you. Doesn't this mean the forces cancle one another, making acceleration impossible?

To "cancel one another", two forces would have to act on the same object. The action-reaction forces we talk about with Newton's Third Law -- or the forces in this question -- act on different objects.

Ex 5.17 Suppose two carts, one twice as massive as the other, fly apart when the compressed spring that joins them is released. How fast does the heavier cart roll compared to the lighter cart?

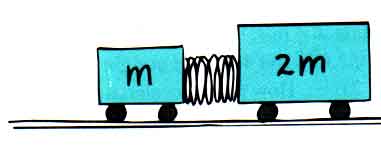
According to Newton's Third Law, the forces on these two masses must be equal (and in opposite directions). According to Newton's Second Law, F = m a, we find a = F / m. That means the acceleration of the twice-as-massive cart will be one-half the acceleration of the other.

Ex 5.19 If a Mack truck and Honda Civic have a head-on collision, upon which vehicle is the impact force greater? Which vehicle experiences the greater acceleration?

The force will be the same on the two vehicles, according to Newton's Third Law. That means the Civic, with far less mass, will experience a much greater acceleration, according to Newton's Second Law.

Ex 5.23 Consider a tug-of-war on a smooth floor between boys wearing socks and girls wearing rubber soled shoes. Why do the girls win?

The girls can exert a greater force with their rubber soled shoes so they will win.

Ex 5.24 Two people of equal mass attempt a tug-of-war with a 12-m rope while standing on frictionless ice. When they pull on the rope, they each slide toward each other. How do their accelerations compare and how far does each person slide before they meet?

The force on each will be the same so they will always have the same acceleration -- and, because of that, the same velocity and they will move the same distance. Thus they will meet in the middle so each will have to move 6 m.

Ex 5.28 When two vectors sum to zero, how must they be related?

They must be equal in magnitude and exactly opposite in direction.

Ex 5.32 If you are standing in a bus that moves at constant velocity and drop a ball from your outstretched hand, you will see its path as a vertical straight line. How will the path appear to a friend standing on the side of the road?

The friend beside the road will see a horizontal component of its motion. He/She might describe this by saying it moves in a "arc" or along a "curved path". Careful observation would show it moves along a "parabolic path". We'll talk about this more in a later chapter on Nonlinear Motion.

Pb 5.1 A boxer punches a sheet of paper in mid-air, and brings it from rest up to a speed of 25 m/s in 0.05 s. If the mass of the paper is 0.003 kg (that is, 3 grams), what force does the boxer exert on it?

F = m a

But what's the acceleration, a?

a = v / t

a = (25 m/s) / (0.05 s)

a = 500 m/s/s

a = 500 m/s

Pb 5.2 If you stand next to a wall on a frictionless skateboard and push the wall with a force of 30 N, how hard does the wall push on you? If your mass is 60 kg, what is your acceleration?

From Newton's Third Law, we know the wall reacts by pushing back on you with a force of 30 N.

F = 30 N

From Newton's Second Law, we can calculate the acceleration that produces,

F = ma

a = F / m

a = (30 N) / (60 kg)

a = 0.5 m/s²

Pb 5.3 If raindrops fall vertically at a speed of 3 m/s and you are running at 4 m/s, how fast do they hit your face?

We will need a vector addition diagram for this. While the raindrops fall down at 3 m/s, they also appear to be moving horizontally at 4 m/s because you are running horizontally at 4 m/s. We will draw vectors (or arrows) to represent these velocities,

You might think of starting by drawing in the velocity vector of 3 m/s downward first and then, at the end of that vector, start the 4 m/s horizontal vector. The resultant vector is then the vector you draw that starts where your diagram started and ends where your diagram ended.

Or you might think of starting by drawing in the the 4 m/s horizontal vector first and then, at the end of that vector, start the 3 m/s downward velocity vector. The resultant vector is then the vector you draw that starts where your diagram started and ends where your diagram ended.

For all of these vector addition diagrams, the resultant, the vector sum of these two velocities, is 5 m/s at an angle of 37 degrees from the horizontal.

Pb 5.6 A canoe is paddled at 4 km/h directly across a river that flows at 3 km/h as shown in the sketch.

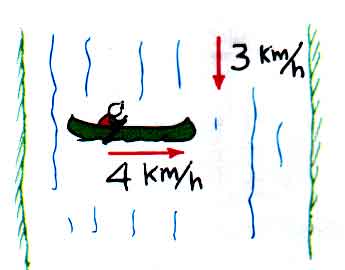
(a) What is the resultant speed of the canoe relative to the shore?

This calls for another vector addition diagram. This is very much like the previous one!

For any of these vector diagrams, the net result, the resultant, the vector sum of these velocities is that the canoe moves across the river at 5 km/h at an angle of 37 degrees south of east or 53 degrees east of south (or 37 degrees as shown in the diagram).

(b) In approximately what direction should the canoe be paddled to reach a destination across the river?

Of course this will requir another vector addition diagram. But this one is more fun. We want the resultant to be horizontal (or east). We know how fast the canoe can travel ( that's 4 km/h ) but we don't know the direction. At what direction do we need to paddel the canoe at 4 km/h so that when the river flows down (or south) at 3 km/h, the resultant velocity will be horizontal (or east)?

Typical multiple-guess questions:

1. The action-reaction forces we encounter in Newton's Third Law

a) always cancel each other out.

b) always act on different objects.

c) are always the same as friction and support forces.

d) may be perpendicular to each other.

2. Newton's Third Law applies

a) only to objects at rest (like pushing on a wall)

b) to object pairs of which at least one must be at rest (like striking a wall with a moving ball)

c) to any two objects that interact

d) only to pairs of objects for which one is much more massive than the other.

3. Newton's Third Law is

a) a special case of Newton's Second Law.

b) a special case of Newton's First Law.

c) independent of Newton's other Laws of Motion.

d) applicable only when air resistance can be neglected.

4. The resultant of two vectors is

a) the smaller of the two vectors.

b) the average of the two vectors.

c) the vector sum of the two vectors.

d) the larger of the two vectors.

5. Vectors may be added

a) like ordinary numbers.

b) by multiplying their magnitudes.

c) by subtracting their magnitudes and multiplying their units.

d) by constructing a vector addition diagram.

Typical multiple-guess questions with answers:

1. The action-reaction forces we encounter in Newton's Third Law

a) always cancel each other out.

b) always act on different objects.

c) are always the same as friction and support forces.

d) may be perpendicular to each other.

2. Newton's Third Law applies

a) only to objects at rest (like pushing on a wall)

b) to object pairs of which at least one must be at rest (like striking a wall with a moving ball)

c) to any two objects that interact

d) only to pairs of objects for which one is much more massive than the other.

3. Newton's Third Law is

a) a special case of Newton's Second Law.

b) a special case of Newton's First Law.

c) independent of Newton's other Laws of Motion.

d) applicable only when air resistance can be neglected.

4. The resultant of two vectors is

a) the smaller of the two vectors.

b) the average of the two vectors.

c) the vector sum of the two vectors.

d) the larger of the two vectors.

5. Vectors may be added

a) like ordinary numbers.

b) by multiplying their magnitudes.

c) by subtracting their magnitudes and multiplying their units.

d) by constructing a vector addition diagram.