CHAPTER 9
Haute CuisineTOC
And there on rafters high
it came that all
who floated up beyond
were prized and shortly
feasted on
What is an Orb?TOC
I begin this section
with some definitions which should help in the discussion of using
the web safely and wisely with students. Every
orbit is defined with respect to some webpage. The orbit
of a webpage is defined to be the set of all webpages that can be
reached using anchors/hyperlinks. For many
webpages, the orbit is so large as to be impossible to comprehend.
For other websites, it may simply be the page itself. I will refer
to a webpage with no external hyperlinks as a dead-endpage. A
dead-endpage is not necessarily a bad thing, especially if we are
concerned about students wandering away from safe places.
A closed orbit is a website with a set of
connecting pages that does not have any hyperlinks to external
sites. Once you reach such a website, you remain at that website
until you use the browser's navigation bar to back out. You can
also exit a closed orbit by using the history list, or a bookmark,
or simply by entering a new URL address. The advantage of closed
orbits is that the students can explore more freely without the
dangers of accidentally finding inappropriate material.
What is a Strand?TOC
A strand is a string or list of pages. If
the pages are given in order, as in the example
Webbing/Projects/page1.htm,

Java Task Bar
then we say that the strand is ordered.

Pointing to Forward Changes the Image

Clicking on Forward Changes the Page
Here an example of three infopages with an additional
help-page. The list of pages is ordered except for the help-page
which can be reached from any other page. The task bar allows the
user to go from one page to another but only in order. This system
is something like a book. On the other hand, the way in which you
access page in an orbit can be very complicated. For instance, you
may be able to access any page in the strand from any other page.
See
Webbing/Projects/toc.htm,
for an example which does not use in line images.

A Table of Contents Strand
In general, a strand is any path within an orbit, or orb. The
orb-web is thus made up of all of its strands, just like a spiders
web. Below, I have placed the diagram of the orbit for the website
which begins at
Webbing/Projects/page1.htm
Note that the arrows indicate when it is possible only to go in one
direction. The other lines indicate that it is possible to move
between pages in either direction. I will call this kind of
diagram a network-graph. This network-graph completely describes
the orbit system. On the other hand, if I have a network-graph,
not too complicated mind you, then I can create an orbit of
webpages that corresponds to it.
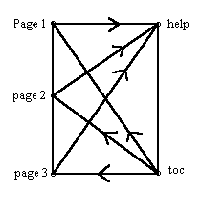
Orbit of Page 1
As you can see, if you study the network-graph, the toc-page has a
hyperlink to each page, and each page has a hyperlink to the
help-page. Pages one through three are linked in order.
Is HTML a Programming Language?TOC
Actually, programming in web documents is usually done in a
portable language such as Java. However, it is
possible to do some simple programming using HTML and your browser.
The programming technique consists mainly of transferring control
of the program from one webpage to another using anchors.
To program
using HTML requires a little care and usually several webpages.
Since HTML is such a simple language, it does not lend
itself to computation or complex interactions. Still, one can often
use the concept of hyperlinks to create some interesting
computer games. An example of one such game is furnished
by the Koenigsberg Bridge Problem introduced
in the chapter on browsers.
The game is really a network-graph, which
is described by the adjacent diagram.
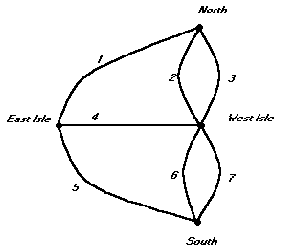
Koenigsberg Bridge Problem Network Graph
There are four points, or places, in Koenigsberg and seven paths,
or bridges, between them. The curves in the diagram represent the
bridges, while the points represent the different places that the
player might be. The actual program consists of 19 webpages. The
first page is the homepage for the game. The homepage allows the
player to select a starting position: north shore; south shore;
east isle; west isle. Once a position has been chosen, the player
must choose an adjacent bridge to cross. There are two pages needed
for each bridge crossed. Consequently, the game is really an
application of HTML and the browser software. Any problem which can
be understood as a network-graph can be implemented as a closed
orbit website.
The Sliding Wooden
PuzzleTOC
As a second example, consider a sliding wooden puzzle. The most common
type of this sort of puzzle is a three by three square with 8 sliding
tiles and one blank space.
\input fswp8.tex
By the way, this example was generated without using In-line
images. To simplify the problem we will consider a sliding wooden
puzzle with only 5 sliding pieces. You would need over 700 webpages
to construct the example with 8 sliding pieces. This tally counts
several similar positions as the same. The actual total number of
distinct positions for an 8 piece sliding wooden puzzle is 5040.
On the other hand, if we use 5 sliding pieces we need only 12
webpages to show the different positions. Recall that when you play
with the sliding wooden puzzle you can always move the pieces in a
" circle."
When you do this, you are not really
changing the positions of the pieces with respect to one another.
A typical move involves centering the blank position and the
piece you wish to move and then sliding that piece either up or
down. For instance suppose we wish to move the piece labeled 3.
Sliding Wooden Puzzle
Click on a piece to move it two spaces.
A Picture of the Sliding Wooden Puzzle
This can be accomplished by circling until the 3 is centered as
below :
Sliding Wooden Puzzle
Click on a piece to move it two spaces.
Center the Three
and then the piece sliding down.
Sliding Wooden Puzzle
Click on a piece to move it two spaces.
Center the Three
All of the
possible moves are like this, and we will always show the move after
the piece labeled 1 has been moved back to the front by circling.
Sliding Wooden Puzzle
Click on a piece to move it two spaces.
Circle Back
The network graph for this example is given below. We have included
it for the interested reader, but you do not need the graph to play
the game. The network graph lies in a sphere and so I have placed
the graph on a Mercator projection.
Think of the pages in the orbit as countries and the curves as
sailing routes between the countries. There are 12 countries. One
at the North Pole and one at the South Pole. Five countries in the
northern hemisphere and five in the southern hemisphere.
Just as in the game you can not reach every country directly.
Sometimes you must go to an intermediate country first. The
slightly complicated nature of the graph makes the game
interesting. Can you tell by looking at the graph, how many
countries you must go through to get from the North Pole to the
South Pole. Note that the South Pole is the winning position.
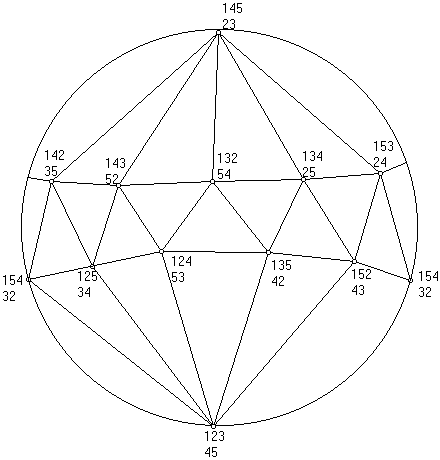
Sliding Wooden Puzzle Network Graph
You must go through 3 countries. Likewise, if you move wisely
you will always solve the
5 piece sliding wooden puzzle in three moves or less.
Not unlike the graph of countries on the globe,
there is one point which appears at the extreme
western and eastern ends of the map. Don't forget
that this is only one point, not two.
Mathematicians often analyze problems in this fashion in order
to solve them. A similar, though much more difficult problem is the
Rubrik's cube. The Rubrik's cube problem can be solved by
considering all the possible moves and the network graph associated
to the problem. Only simple problems of this kind can be
implemented using webpages and browsers.
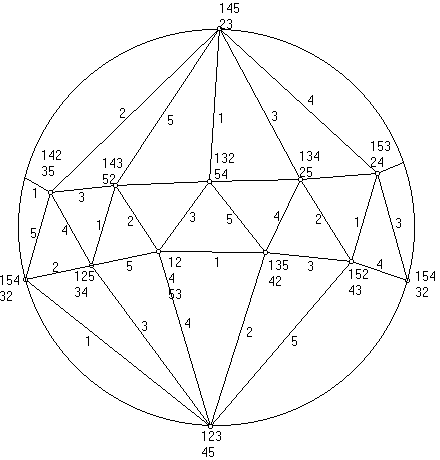
Sliding Wooden Puzzle Solution
You can now see the complete solution of the 5 piece sliding wooden
puzzle problem. The path from one position to another is marked by
the number of the piece that must be moved. You can verify the
table by starting at the sliding wooden puzzle homepage on the
floppy disk at
kbpg/swp.htm
A Simple JavascriptTOC While many of the
browsers handle precompiled JAVA applets it is
also possible to write simple programs using
javascript. Be aware that not all browsers handle
javascript, but if you are mainly interested in demonstrating the
power of the web to your students, then javascript will provide
the opportunity. I have constructed a simple example of javascript
and the resulting homepage at
Webbing/Projects/javex.htm
using the Task-bar template. The program will run correctly on
Netscape 3.0, but probably not on most other browsers. The idea of
the program is to have the browser "color"
\hskip0.2truecm the hyperlink when the mouse passes over it. To do
this, I first write a script carefully in the
HEAD section of the HTML document. I use comments around
the entire script so that a browser which does not use the script
will ignore it.
<HEAD>
<TITLE> Java Taskbar HP </TITLE>
<script language="Javascript1.1">
<!--
function ImgChange(imgNum,imgSrc) {
document.images[imgNum].src = imgSrc;
}
// -->
</script>
</HEAD>
The script creates an object which is denoted by the word "
function." \hskip0.5truecm In this case, the object has two parts.
The first part tells the java-interpreter which image to change.
The second part tells the java-interpreter which image to use when
a change is made. The rest of the script tells the interpreter how
to find the image numbers in the document. Note that the document
counter starts counting the images with the number 0, not 1. Later
in the document the function is applied when the mouse passes over
an anchor position. In this case, the anchor/image that I wish to
change. This is accomplished by the javascript words "onMouseOver "
and "onMouseOut".
<a href="javex2.htm"
onMouseOver="ImgChange(2,'forwl.gif');"
onMouseOut="ImgChange(2,'forw.gif');">
<IMG SRC="forw.gif" BORDER=0 > </a>
The end result is that when the mouse pointer passes over the
anchor/image the "ImgChange" function takes control and replaces
the image on your screen.
Below is an example of this type of page except that the anchors
will not move to another page.
|