Ch 19, Temperature

Homework Solutions:

Ch19: Questions 5, 9, *, 16, 17

Ch19: Problems *, **, 18, 25, 27, 40, 47, 50, 64

---

19.Q5: Why should the amalgam used in dental fillings have the same average coefficient of thermal expansion as a tooth? What would occur if they were mismatched?

Think of what would happen if the coefficients of thermal expansion for the tooth and the filling amalgam were not the same. Then they would expand differently as the temperature changed. This would cause stress -- and pain!

19.Q9: Markings to indicate length are placed on a steel tape in a room that has a temperature of 22^oC. Are measurements made with the tape on a day when the temperature is 27^oC greater than, less than, or the same length as the object's length?

At 27^oC, the tape is now longer and the distance or spacing between the markings are longer or farther apart. This means the tape will measure a smaller numer or a lower number. Objects measured under these conditions will be measured to have a smaller length.

19.*: The pendulum of a certain pendulum clock is made of brass. When the temperature increases, does the clock run too fast, run too slowly, or remain unchanged?

Brass? Actually, the concept is exactly the same whether we are dealing with brass or steel or aluminum. As the temperature increses, the length of the pendulum also increases. With an increased length, the period of the pendulum is also increased. As the pendulum oscillates more slowly, the clock keeps time more slowly.

19.Q16: And automobile radiator is filled to the brim with water when the engine is cool. What happens to the water when the engine is running and the water is heated? What do modern automobiles have in their cooling systems to prevent the loss of coolants?

As the temperature of the engine coolant increases, the volume also increases. Today's automobiles have a plastic "overflow resevior" that the coolant flows into. Later, as the coolant cools, the pressure decreases and coolant is "pulled" our "suctioned" from this "overflow reservior" back into the radiator.

19.Q17: Metal lids on glass jars can often beloosened by running them under hot water. How is this possible?

The coefficient of thermal expansion is much greater for metals than for glass. Heating a metal lid on a glass jar will cause the metal lid to expand far more than the glass. This should allow you to unscrew the metal lid from the glass jar.

---

19.* Convert the following to equivalent temperaturs on the Celsius and Kelvin scales:

(a) the normal human body temperature, 98.6^o F

T_C = (⁵/₉) (T_F - 32)

T_C = (⁵/₉) (98.6 - 32)

T_C = (⁵/₉) (66.6)

T_C = 37^oC

(b) the air temperature on a cold day, - 5^o F

T_C = (⁵/₉) (T_F - 32)

T_C = (⁵/₉) ( - 5 - 32)

T_C = (⁵/₉) ( - 37)

T_C = - 20.6^oC

 

19.** There is a temperature whose numerical value is the same on both the Celsius and Fahrenheit scales. What is this temperature?

T_C = (⁵/₉) (T_F - 32)

T_x = (⁵/₉) (T_x - 32)

T_x = (⁵/₉) (T_x ) - (⁵/₉)(32)

T_x = (⁵/₉) (T_x ) - (⁵/₉)(32)

T_x - (⁵/₉) (T_x ) = - (⁵/₉)(32)

(⁴/₉) (T_x ) = - (⁵/₉)(32)

4 T_x = - 5 (32)

T_x = - (⁵/₄)(32)

T_x = - 40

meaning both

T_x = - 40^oC

and

T_x = - 40^oF

 

19.18 A concrete walk is poured on a day when the temperature is 20.0^oC, in such a way that the ends are unable to move.

(a) What is the stress in the cement on a hot day of 50.0^oC?

(b) Does the concrete fracture?

Take Young's modulus for concrete to be 7.00 x 10⁹ N/m² and the tensile strength to be 2.0 x 10⁹ N/m²

If the ends were free to expand, how much would a section of length L expand?

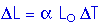
From Table 19.2, p 588, or from Problem 19.10, immediately above, we know that the coefficient of thermal expansion for concrete is

= 12 x 10 ^{- 6} (C^o) - 1

And the temperature difference is

T = 30 C^o

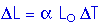
L = [12 x 10 ^{- 6} (C^o) ^{- 1}][ L ][30 C^o]

L = 3.6 x 10 ^{- 4} L

Think back, now, to PHY 1351 and recall what is meant by "stress" and "strain". Stress is the force per unit area and strain is the elongation or compression divided by the area.

Stress = F / A

Strain = L / L

Strain = [ 3.6 x 10 ^{- 4} L ] / L

Strain = 3.6 x 10 ^{- 4}

Y = Stress / Strain

Stress = [ Y ] [ Strain ]

Stress = [ 7.00 x 10⁹ N/m² ] [ 3.6 x 10 ^{- 4} ]

Stress = 2.52 x 10 ⁶ N/m²

Tensile Strength = 2.0 x 10⁹ N/m²

This thermal stress is much, much less than the tensile strength so the concrete does not break.

 

19.25 The concrete sections of a certain superhighway are designed to have a length of 25.0 m. The sections are poured and cured at 10.0^oC. What minimum spacing should the engineer leave between the sections to eliminae buckling of the concrete is to reach a temperature of 50.0^oC?

How much witll the 25.0 m section expand as the temperature changes from 10.0^oC to 40.0^oC?

For concrete, the coefficient of thermal expansion is 12 x 10 ^{- 6} (C^o) ^{- 1} (from Table 19.2, on p 588) ;

= 12 x 10 - 6 (C^o) - 1

The temperature change, T, is 40 C^o;

T = 40 C^o

Now we can put all the pieces together and evaluate the expansion, L ;

L = [12 x 10 - 6 (C^o) - 1][25.0 m][40 C^o]

L = 0.012 m

L = 1.2 cm

Since each concrete section will expand by 1.2 cm, there must be 1.2 cm between each section so they do not run into each other and cause compressive stresses.

 

19.27 At 20.0^oC, an aluminum ring has an inner diameter of 5.000 0 cm and a brass rod has a diameter of 5.050 0 cm.

(a) To what temperature must the ring be heated so that it will just slip over the rod?

We need to increase the diameter of the aluminum ring from L_o = 5.000 0 cm (or L_o = 5 x 10 ^{- 2} m) to 5.050 0 cm. That is an increase of

L = 0.050 cm = 5 x 10 ^{- 4} m

From Table 19.2, p 588, we find that the coefficient of thermal expansion for aluminum is

= 24 x 10 ^{- 6} (C^o) ^{- 1}

L = L_o T

T = [L ] / [ L_o ]

T = [ 5 x 10 ^{- 4} m ] / [ ( 24 x 10 ^{- 6} (C^o) ^{- 1} ) ( 5 x 10 ^{- 2} m )]

T = 417 C^o

T_f = 437 ^o C

(b) To what common temperature must the two be heated so that the ring just slips over the rod? Would this latter process work?

Now we are going to heat both the aluminum ring and the brass rod. Both will expand. We must heat them until the expansion of the aluminum ring diameter is 5 x 10 - 4 m greater than the expansion of the brass rod diameter.

aluminum ring Al = 24 x 10 - 6 (Co) - 1 LAl = LoAL T LAl = ( 24 x 10 - 6 (Co) - 1)(5 x 10 - 2 m) T

brass rod Br = 19 x 10 - 6 (Co) - 1 LBr = LoBr T LBr = ( 19 x 10 - 6 (Co) - 1)(5.05 x 10 - 2 m) T

Now set

L_Al =L_Br + 5 x 10 - 4 m

( 24 x 10 ^{- 6} (C^o) ^{- 1})(5.00 x 10 ^{- 2} m) T = ( 19 x 10 ^{- 6} (C^o) ^{- 1})(5.05 x 10 ^{- 2} m) T + 5 x 10 ^{- 4} m

( 24 x 10 ^{- 6} (C^o) ^{- 1})(5.00) T = ( 19 x 10 ^{- 6} (C^o) ^{- 1})(5.05) T + 5 x 10 ^{- 2}

( 24 x 10 ^{- 6})(5.00) T = ( 19 x 10 ^{- 6})(5.05) T + 5 x 10 ^{- 2} C^o

( 24)(5.00) T = (19)(5.05) T + 5 x 10 ^{+ 4} C^o

120 T = 96T + 5 x 10 ^{+ 4} C^o

24 T = 5 x 10 ^{+ 4} = 50,000 C^o

T = 2,080 C^o

T = 2,100^oC

Is this practical? It's difficult to even handle objects at this temperature! This may even be close to the melting temperature of either of the materials.

19.40 A tank having a volume of 0.100 m³ contains helium gas at 150 atm. How many balloons can the tank blow up if each filled balloon is a sphere 0.300 m in diameter at an absolute pressure of 1.20 atm?

d = 0.300 m

r = d/2 = 0.150 m

First, the easy part; what is the volume of each balloon?

V_bal = (⁴/₃) r³

V_bal = (⁴/₃) (0.150 m)³

V_bal = 0.0141 m³

How many moles of helum are in each individual balloon?

P V = n R T

n = P V / R T

n_bal = [(1.2 atm)(0.0141 m³ )] / [(0.082 L-atm/mol-K)(T)]

While we do NOT know the temperature T, it won't make any difference since the tank and the balloons are at the same temperature.

n_bal= 0.207 moles/T

(Remember, this has strange units simply because we do not know the temperature T).

Now let us return to the tank and determine how many moles of helum are in the tank.

P V = n R T

n = P V / R T

n_tnk = [(150 atm)(0.100 m³ )] / [(0.082 L-atm/mol-K)(T)]

n_tnk = 183 moles/T

(Again, these units look strange simple because we do not know the temperature T).

The number of balloons N, then is

N = n_tnk / n_bal

N = 183 / 0.207

N = 884 balloons

 

19.47 An automobile tire is inflated with air originally at 10.0^oC and normat atmospheric pressure. During the process, the air is compressed to 28.0% of its original volume and its temperature is increased to 40.0^oC.

(a) What is the tire pressure?

P V = n R T

n R =P V / T = const

P₂ V₂ / T₂= P₁ V₁ / T₁

Remember, these temperatures must be absolute temperatures, measured in kelvins!

T₁ = 10^oC = 283 K

T₂ = 40^oC = 313 K

V₂ = 0.28 V₁

P₁ = 1.0 atm

P₂ = ?

P₂ V₂ / T₂ = P₁ V₁ / T₁

P₂ = P₁ [ (V₁ / V₂) (T₂ / T₁) ]

P₂ = 1.0 atm [(V₁/0.28 V₁) (^{313 K}/ _{283 K})]

P₂ = 1.0 atm [(¹/_0.28)(³¹³/₂₈₃)]

P₂ = 1.0 atm [3.95]

P₂ = 3.95 atm

(b) After the car is driven at high speed, the tire air temperature rises to 85.0^oC and the interior volume of the tire increases by 2.00%. What is the new (absolute)tire pressure in pascals?

The values T₁, P₁, and V₁ remain the same; but for this part T₂, V₂, and P₂ are new.

T₂ = 85^oC = 358 K

V₂ = (1.02)V_2old = (1.02)(0.28 V₁)

V₂ = 0.286 V₁

P₂ = ?

P₂ V₂ / T₂ = P₁ V₁ / T₁

P₂ = P₁ [ (V₁ / V₂) (T₂ / T₁) ]

P₂ = 1.0 atm [(V₁/0.286 V₁) (^{358 K}/ _{283 K})]

P₂ = 1.0 atm [(¹/_0.286)(³⁵⁸/₂₈₃)]

P₂ = 1.0 atm [4.43]

P₂ = 4.43 atm

 

19.50 A cylinder is closed by a piston connected to a spring of constant 2.0 x 10³ N/m. While the spring is relaxed, the cylinder is filled with 5.00 L of gas at a pressure of 1.00 atm and a temperature of 20.0^oC.

(a) If the piston has a cross-sectional area of 0.010 0 m² and a negligible mass, how high will it rise when the temperature is increased to 250^oC?

(b) What is the pressure of the gas at 250^oC?

Caution: Remember "absolute pressure" and "gauge pressure"? When the pressure inside the cylinder is an absolute pressure of 1.0 atm, the "gauge pressure" is zero and the force the spring exerts is zero. This means the spring is not compressed.

F_spring = k x

F_outside = (1.0 atm)A + F_spring

F_outside = F_inside = F_piston

F_outside = F_piston

F_piston = P A

(1.0 atm)A + F_spring = F_piston

P V = n R T

n = P V / R T

n = (1.0 atm)(5.0 L) / [ (0.082 L-atm / mol-K) (293 K)]

n = 0.208 moles

P = n R T / V

What is the new volume? And what is the new pressure? Be sure to use the new temperature in units of kelvins.

V = 5.0 L + A x

V = 5.0 L + ( 0.010 0 m²) x

T = 250^oC = (250 + 273) K = 523 K

P = n R T / V

P = ( 0.208 moles) (0.082 L-atm / mol-K) (523 K)/ [ 5.0 L + ( 0.010 0 m²) x]

P = 8.92 L-atm / [ 5.0 L + ( 0.010 0 m²) x]

(1.0 atm)A + F_spring = F_piston

F_spring = k x = ( 2.0 x 10³ N/m ) x

F_piston = P A = { 8.92 L-atm / [ 5.0 L + ( 0.010 0 m²) x ] } { 0.010 0 m²}

(1.0 atm)A + F_spring = F_piston

(1.0 atm)A + (2.0 x 10³ N/m) x = { 8.92 L-atm / [ 5.0 L + ( 0.010 0 m²) x ] } { 0.010 0 m²}

Be careful with the units! We were given a volume as 5.0 L and an initial pressure of 1.0 atm so it seems "reasonable" to use R in units of L-atm/mol-K. But we also have a spring constant k in units of N/m so it would also be "reasonable" to use R in units of J/mole-K. In either case, conversions will be required!

(1.0 atm)A + (2.0 x 10³ N/m) x = 0.0892 L-atm-m²/ [ 5.0 L + ( 0.010 0 m²) x ]

(1.0 atm)(0.010 0 m²) + (2.0 x 10³ N/m) x = 0.0892 L-atm-m²/ [ 5.0 L + (0.010 0 m²) x ]

From page 465, we know that

1.0 atm = 1.013 x 10 ^{+ 5} Pa = 1.013 x 10 ⁵ N/m²

(1.013 x 10 ⁵ N/m²)(0.010 0 m²) + (2.0 x 10³ N/m) x = 0.0892 L-atm-m²/ [ 5.0 L + (0.010 0 m²) x ]

(1.013 x 10 ³ N) + (2.0 x 10³ N/m) x = 0.0892 L-atm-m²/ [ 5.0 L + (0.010 0 m²) x ]

(1.013 x 10 ³ N) + (2.0 x 10³ N/m) x = 0.0892 L(1.013 x 10 ⁵ N/m²)m²/ [ 5.0 L + (0.010 0 m²) x ]

1 013 N + (2.0 x 10³ N/m) x = 9 036 L-N/ [ 5.0 L + (0.010 0 m²) x ]

1.0 L = 1,000 cm³ = 0.001 m³ = 10 ^{- 3} m³

1 013 N + (2.0 x 10³ N/m) x = 9 036 N/ [ 5.0 (10 ^{- 3} m³) + (0.010 m²) x ]

1 013 N + (2.0 x 10³ N/m) x = 9 036 (10 ^{- 3} m³)N/ [ 5.0 x10 ^{- 3} m³ + (0.010 m²) x ]

1 013 N + (2.0 x 10³ N/m) x = 9 .036 m³-N/ [ 5.0 x10 ^{- 3} m³ + (0.010 m²) x ]

1 013 + (2.0 x 10³ 1/m) x = 9 .036 m³/ [ 5.0 x10 ^{- 3} m³ + (0.010 m²) x ]

1 013 + (2.0 x 10³ 1/m) x = 9 .036 / [ 5.0 x10 ^{- 3} + (0.010 m ^-1) x ]

If we require that the distance x also be measured in meters, then we can write this equation as

1 013 + (2.0 x 10³ ) x = 9 .036 / [ 5.0 x10 ^{- 3} + 0.010 x ]

[1 013 + 2 000 x] [0.005 + 0.010 x ] = 9 .036

5.065 + 10.13 x + 10 x + 20 x² = 9.036

20 x² + 20.13 x + 5.065 = 9.036

20 x² + 20.13 x - 3.97 = 0

Finally, we have something that looks familiar. Now we can use the quadratic formula with a = 20, b = 20.13, and c = - 3.97 .

x = { - b SQRT[ b² - 4 a c] }/ 2 a

x = { - 20.13 SQRT[ (20.13)² - 4 (20)( - 3.97 ) ] }/ [ 2 (20) ]

x = { - 20.13 SQRT[ 405.2 + 317.6 ] }/ 40

x = { - 20.13 SQRT[ 722.8] }/ 40

x = { - 20.13 26.88 }/ 40

x₁ = 0.17 m = 17 cm or x₂ = - 1.175 m

The positive distance is the physically significant one. The negative value satisfies the mathematics but not the Physics; it is an extraneous solution.

x = 17 cm

Now, what about the new pressure? We could solve for that with the Ideal Gas Law. Let's use that as a "check". It seems easier to use the compression of the spring to find the new pressure.

F_outside = (1.0 atm)A + F_spring

F_outside = F_inside = F_piston

F_outside = F_piston

F_piston = P A

P A = (1.0 atm)A + k x

P = 1.0 atm + k x / A

P = 1.0 atm + (2.0 x 10³ N/m)(0.17 m) / 0.010 m²

P = 1.0 atm + 3.4 x 10 ⁴ N/m²

P = 1.0 atm + 3.4 x 10 ⁴ Pa [ 1 atm / 1.013 x 10⁵ Pa]

P = 1.33 atm

We can check this -- and our entire calculation -- by checking this result with the result we get for the new pressure using the Ideal Gas Law. Now that we have solved for x, the linear distance of expansion of the piston, we can easily solve for the new volume.

V = A x = (0.010 m²) (0.17 m)

V = 0.001 7 m³

V = [ 0.001 7 m³ ] [ 1.0 L / 0.001 m³ ]

V = 1.7 L

Thus, the new volume is

V = V_o +V

V = 5.0 L + 1.7 L

V = 6.7 L

P V = n R T

P = n R T / V

P = (0.208 moles)(0.082 L-atm/mol-K) (523 K) / 6.7 L

P = 1.33 atm

19.64 A steel ball bearing is 4.000 cm in diameter at 20.0^oC. A bronze plate has a hole in it that is 3.994 cm in diameter at 20.0^oC. What common temperature must they have so that the ball just squeezes through the hole?

steel ball bearing Al = 11 x 10 - 6 (Co) - 1 LSt = LoSt T LSt= LoSt+ L LSt = LoSt ( 1 + T ) LSt = [4.000 cm] [ 1 + ( 11 x 10 - 6 (Co) - 1)T ]

bronze plate Br = 19 x 10 - 6 (Co) - 1 LBr = LoBr T LBr= LoBr + L LBr = LoBr ( 1 + T ) LBr = [3.994 cm] [ 1 + ( 19 x 10 - 6 (Co) - 1)T ]

L_St = L_Br

[4.000 cm] [ 1 + ( 11 x 10 ^{- 6} (C^o) ^{- 1})T ] = [3.994 cm] [ 1 + ( 19 x 10 ^{- 6} (C^o) ^{- 1})T ]

4.000 cm + [4.000 cm] [ ( 11 x 10 ^{- 6} (C^o) ^{- 1})T ] = 3.994 cm + [ 3.994 cm] [ ( 19 x 10 ^{- 6} (C^o) ^{- 1})T ]

0.006 cm + (4.000 cm) ( 11 x 10 ^{- 6} (C^o) ^{- 1})T ] = (3.994 cm) ( 19 x 10 ^{- 6} (C^o) ^{- 1})T ]

0.006 cm + 4.4 x 10 ^{- 5} T cm (C^o) ^{- 1} = 7.58 x 10 - 5 T cm (C^o) ^{- 1}

0.006 cm = [(7.58 x 10 ^{- 5}) - ( 4.4 x 10 ^{- 5})] [ T cm (C^o) ^{- 1]}

0.006 cm = [(3.18 x 10 ^{- 5})] [ T cm (C^o) ^{- 1]}

0.006 = [(3.18 x 10 ^{- 5})] [ T (C^o) ^{- 1]}

(3.18 x 10 ^{- 5}) [ T (C^o) ^{- 1}] = 0.006

(3.18 x 10 - 5)T = 0.006 C^o

T = 0.006 C^o / 3.18 x 10 ^{- 5}

T = 189^oC

 

Summary			Ch20, Heat
Return to Temperature ToC

(c) Doug Davis, 2002; all rights reserve