Indirect Arguments (And a New Test of Validity)
I. Indirect Arguments. When we want to argue for some conclusion, it looks like we only have one option: provide evidence (premises), which the conclusion follows from. But here I will present a radical alternative – a method of proving a conclusion without ever providing any evidence for that conclusion. This new argument strategy will be a round-about method of proving a conclusion, a way of sneaking up on the conclusion indirectly; and that’s why this new argument strategy is called an indirect argument.
Here’s the idea: we have some controversial issue we're arguing about, like “Does God exist?” or “Do you owe me $20?” Since it's a Yes/No question, there are two direct answers to it:

For example:

Now in the abstract, before we look at any evidence, all answers are created equal – we could pick either possible answer to the question. So how do we pick – what tips the scales in favor of one answer (the right one) over the other (the wrong one)? Clearly, the evidence does: the premises tip the scales of reason in favor of that conclusion.
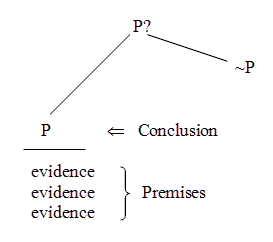
That's the typical pictures of arguments: if you want to argue for “P” (over “~P”), you provide evidence that supports “P”. Here we are arguing directly for “P”: providing evidence that leads directly to “P”.
But now consider an alternate route to the conclusion, “P”. Instead of providing evidence for “P”, we can provide evidence against the competing conclusion, “~P”. Thanks to the Principle of Bivalence (plus the semantic rule for negations), we know that either “P” will be true, or (if “P” is false) that “~P” will be true – but not both. If we can provide evidence ruling out “~P” – evidence showing that “~P” must be false – then “P” will be the only option left standing. By ruling out the alternative, we will show that “P” must be true. In that case, we won't have directly provided evidence for “P”. Instead, by ruling out the alternative, we will have proven “P” indirectly.
First Question: What will count as evidence that “~P” is false? We need show that “~P” leads logically to unacceptable conclusions – that is, we need to show that, if you believe “~P,” you’ll be committed to certain consequences of “~P” that are absolutely unbelievable. If believing “~P” commits you, in the bargain, to a totally unacceptable conclusion, then you’d better not believe “~P”. So you’d better believe “~P” is false. And if you believe that “~P” is false, then you’d better believe that “P” is true.
Second Question: How much evidence do we need to provide against “~P,” before we're convinced that it's false, and that “P” is the only viable option? Well, compare it to direct arguments: how much evidence did we need to have in favor of “P,” before we had a valid argument for “P”? In logic, where we’re holding out for validity, the truth of the premises must guarantee the truth of the conclusion. The premises can't just provide pretty good evidence, that makes the conclusion pretty likely. True premises must guarantee a true conclusion, prove it outright.
That doesn't change when we move to indirect arguments. Once again, we must prove “P,” is true, by absolutely ruling out the alternative view, “~P”. So it’s not enough to provide fairly strong evidence against “~P,” that makes “~P” pretty likely to be false. We need evidence that absolutely rules out “~P,” showing that “~P” is definitely false.
So, for example, “~P” can’t just lead to distasteful or unhappy consequences – that's not strong enough evidence, because distasteful and unhappy claims might still be true. Suppose I tried to argue, indirectly, that you owed me $20, like this:
It must be that you owe me $20 (P); because if the opposite were true – if you didn’t owe me $20 (~P) – then I’d have nobody to give me the money for the concert ticket. But I’d find missing the concert to be very distasteful and unhappy – so distasteful and unhappy, in fact, that I simply can’t accept the claim that you don’t owe me $20 (~P). So, then, you must owe me $20 (P).
Now, you know this sort of argument wouldn’t convince you that you owed me $20. Yes, you might say, if I don’t owe you the money, your life may hit a distasteful and unhappy patch. Tough luck: sometimes life is unhappy and distasteful. You know how they say “the truth hurts”? Well, one reason the truth hurts is because the truth can be unhappy and distasteful. Deal with it!
In a lame argument like that, “~P” wouldn't be ruled out, because “~P” wouldn’t be proven false – just shown to be distasteful or unhappy.
Nor would it be enough to show that “~P” leads to startling, hard-to-believe consequences, and for the same reason: sometimes the truth can be startling, and hard-to-believe. Think again of the theory of relativity, or quantum physics: lots of surprising, hard-to-believe consequences follow from such theories, but that certainly wasn't enough to make us think those theories were false.
To rule out “~P,” we will need a consequence from “~P” that is guaranteed to be false. Unhappy and distasteful consequences aren’t guaranteed to be false. Surprising, hard-to-believe consequences aren’t guaranteed to be false.
So what kind of claim is guaranteed to be false in Logic? I’ll tell you what kind: a sentence which violates a fundamental logical principle, a principle which our whole logical system is based upon – now that sort of sentence would be absolutely ruled out in our logical system. And the Principle of Bivalence is just such a fundamental principle for our logical system. Any sentence which goes against the Principle of Bivalence is a sentence automatically ruled out as false by our logical system. So: if “~P” leads to an outright violation of the Principle of Bivalence, then “~P” is guaranteed to be false. And in that case, we would likewise be guaranteed that “P,” as the only remaining option, is true.
Third Question: what does it mean to say that “~P” would “lead to a violation of Bivalence”?
The Principle of Bivalence says:
In any possible situation, a given sentence is either true in that situation, or else false in that situation (not both).
“~P” would lead to a violation of Bivalence if “~P” led us to say that some sentence is both true and false at the same time. If we could show logically that believing “~P” commits you to believing some sentence is both true and false at the same time – then we will have shown that you cannot, in good logical conscience, believe “~P”. And in that case, “P” would be left as the only option standing.
That's the basic idea behind an indirect argument: we prove “P”, not by directly providing evidence for “P,” but by showing that the only other option, “~P,” must be false. And we show that “~P” must be false by considering what happen if we believed “~P”. An indirect argument for “P” would go like this
Suppose you believed “~P” is true. Since “~P” leads you to believe some other sentence is true and false at the same time, believing “~P” forces you to violate the Principle of Bivalence. But you couldn't possibly accept a violation of Bivalence. So you can't possibly believe “~P” is true. So you have no choice but to believe that “P” is true.
We prove “P” indirectly by reducing the alternative, “~P,” to absurdity (a violation of our logical principles). And that's why, back in ancient Latin-speaking days, an indirect argument was called a Reductio Ad Absurdum: you prove a point by reducing its opposite to absurdity.
II. Applying the Indirect Argument Strategy to Validity. You can apply the Indirect Argument strategy to arguments on any topic, as long as you have the right evidence: you can make indirect arguments about birds, clouds, frogs, whatever you want. But a really interesting application of this strategy is to discussions about validity. So far, whenever we wanted to show that a certain argument is valid, we’ve had to show this directly, by building a truth table for that argument. But now we can demonstrate an argument’s validity indirectly.
We will follow the general indirect argument strategy laid out already – though now the controversial question will be whether a certain argument is valid.

We could build a truth table for this argument, and provide direct evidence that the argument must be valid. Or we could, instead, show that the argument is valid indirectly. We follow the same general indirect argument strategy here: assume the opposite (assume that the argument is invalid), and show how that opposite assumption leads to absurdity (a violation of Bivalence). Having done that, we have shown that the opposite assumption must be false – the argument cannot be invalid after all. So only one option remains: the argument must be valid.
That’s the basic idea behind an indirect way of showing that an argument is valid:
(1) Assume the opposite: assume that the argument is invalid.
(2) Show how this opposite assumption leads to a violation of Bivalence. (In other words: show that if this opposite assumption were true – if the argument really were invalid – then some sentence would be true and false at the same time.)
(3) Since a violation of Bivalence is absolutely unacceptable in our logic, this opposite assumption must be false: it must be false to claim that this argument is invalid.
(4) So that leaves only one possibility: since the argument is not invalid, the argument must be valid.
Strange as this may seem at first, we will soon grow to love such an indirect method of showing when an argument is valid.
One More Question: Exactly how do we “show logically” that the opposite assumption leads to a violation of Bivalence (making some sentence true and false at the same time)?
Answer: we use the good old semantic rules that we followed in the truth tables – the semantic rules for negations, conjunctions, and disjunctions. Those three rules, plus the Principle of Bivalence, are all the Logic we needed for the truth table test of validity. And at this point, they’re nothing new: we can repeat the Principle of Bivalence, and the three semantic rules, even when we’re drunk, or half-asleep. So it turns out we won’t need anything new for an indirect test of validity. So what are we waiting for? Let’s try it.