1. New Notation.  We’ve just seen that using Indirect semantic methods can save us a lot of time and effort.  And that’s the real appeal of the Indirect method: we want to avoid as much work as possible.  Now we’ll introduce one more change, for precisely the same reason: to avoid (even more) work.

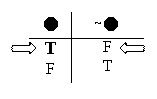
This last change involves the notation we’ve been using in our semantics.   So far we’ve been using T to mark a sentence as true, and F to mark a sentence as false.  That’s not a bad notation, really.  But then again, there’s nothing sacred about that notation, which forces us to use it, rather than using some other notation.  T and F are handy to English speakers such as ourselves, because T is the first letter of the word “true,” and F is the first letter of the word “false”.  (You knew that’s why we’ve been using T and F, right?)  But the T and F notation wouldn’t be that useful in, say, French; there V and F would be easier to remember.  If we’re doing logic with people from various different countries, maybe a language-neutral notation would be best – like “1” for true, and “0” for false.  We can pick whatever notation suits our purposes best.

In the Indirect semantic method, our purpose is to avoid as much work as possible.  So now we’ll introduce a new notation which requires less work: the vertical line notation.

We draw a vertical line, and interpret it in the following way: putting a sentence on the left of that line will mean that the sentence is true; while putting a sentence on the right of the line will mean that the sentence is false.

For instance, if I wanted to picture a situation where “P” and “Q” are both true, while “R” is false, I would write it like this.


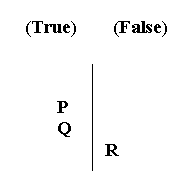
(The words “True” and “False” at the top aren’t really part of the vertical line notation; I’m just writing those in here until we get used to the vertical line.)

We can see right away that using this vertical line notation, instead of the old T and F notation, cuts down on our work.  In the old T/F notation, we have to write each sentence, and then write a T or F to say whether that sentence is true or false.


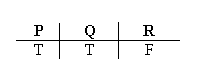
But in our new vertical line notation, you don’t need a T or an F to show whether the sentence is true or false.  You just write that sentence; and where you wrote the sentence (on the left, or the right, of the line) already says whether that sentence is true or false.

Let’s count each sentence, and each T or F, as a separate step we have to go through.  Then showing the situation where “P” and “Q” are true, and “R” is false, took 6 steps in the old T/F notation.  In the vertical line notation, we only have to write the three sentences; even if we count the vertical line as one more step, it still only took us 4 steps to picture the same situation.  4 steps instead of 6: we cut out one-third of our labor!  That’s a serious reduction in the amount of writing we have to do.

And the more sentences we have to deal with, the more the savings increase.   If we were dealing with 10 different sentences, and had to show the truth value of each, the old T/F notation would require 20 steps in all (the 10 sentences, and then 10 T’s and F’s).  With the vertical line notation, the same situation would take only 11 steps to picture (the 10 sentences, and one vertical line).  20 versus 11 – that’s a savings of almost half.

So we will proceed to use the vertical line notation in our semantics.  The indirect test of validity, combined with the vertical line notation, will provide our semantic test of validity with a great savings in labor.


2. The Indirect Test (and the Semantic Rules) Revisited.  What will the indirect test of validity look like, when reformatted in the vertical line notation?  Well, remember how the indirect test proceeds: we start out by assuming that the argument is invalid; that is, we start out by assuming there’s a Validity Counterexample; that is, we start out by picturing a situation where all the premises of the argument are true, but the conclusion is still false.  In our new format, the Validity Counterexample would look like this:


Since left of the line means “true,” and right of the line means “false, ” this is indeed a situation where all the premises are true, and the conclusion is false.

So, for example, we can return to our original argument once more.


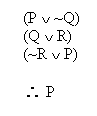
To test this for validity indirectly, using our new notation, we would start out by assuming a Validity Counterexample for the argument, like so:


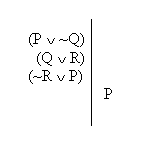
And then we just follow through all the consequences of these truth values, down through smaller and smaller parts, and see if it violates Bivalence.

Except now we have a new problem: what do we use to follow through all the consequences?  The semantics rules, of course.  But (here’s the problem): the semantic rules were all written in our bad old T/F notation.



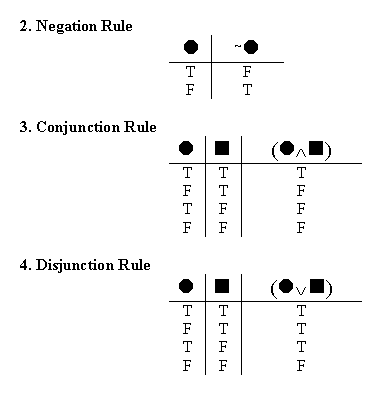
Clearly, we need to re-write these semantic rules in our cool new vertical line notation, so we can use them to chase down consequences in our new-and-improved test of validity.  We don’t want to change any of the results of the semantic rules – we still want negations, for instance, to be true in all the same situations as before.  We just want to write those same old results, in the new notation.

And as long as we’re restating our semantic rules in a new format, let’s make one more change to how we write them out.  Keep in mind, we want to use these semantic rules for chasing down consequences, in our Indirect test of validity.  And as we’ve seen, the indirect test of validity moved in the opposite direction of the old truth-table test: while truth tables started with the smallest parts (sentence letters) and built up to the wholes (the premises and conclusion), the indirect test proceeded in reverse – starting with the wholes (the premises and conclusion), and following down to the parts (ultimately, the sentence letters).  So, in order to match the semantic rules up perfectly with the indirect test, let’s not only rewrite these semantic  rules in our new vertical line notation, but also write them in a whole-to-part way.

That’s not as hard as it might sound.  Start with the semantic rule for negations.



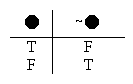
In the old days we read this rule from left to right – from the part (“ ”) to the whole (“~ ”).  To read it instead from whole to part, we just read it in the opposite direction – from right to left.

Look at the first valuation.  That’s a situation where “~ ” is false.


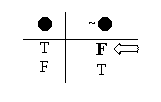
We see that when “~ ” is false, “ ” must be true.


Now say that again, in the vertical line notation.

If “~ ” is false…


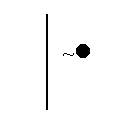
then “ ” must be true.



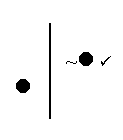
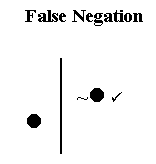
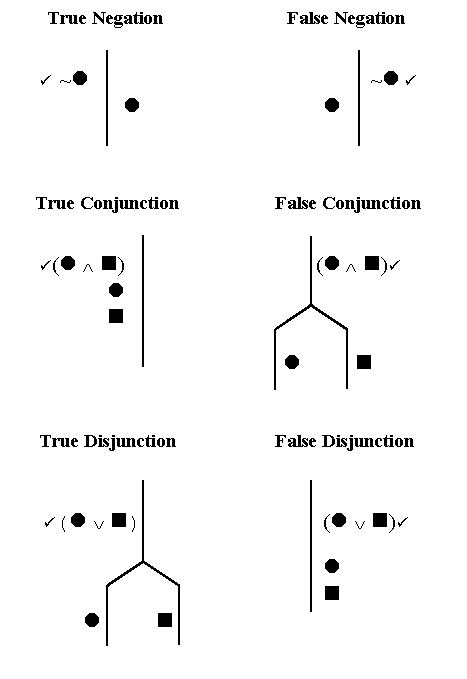
That’s how every false negation works, according to our traditional semantic rule for negations; and that doesn’t change just because we’re using the vertical notation.  And since this is the rule for false negations, we call this the False Negation Rule


And if you liked the False Negation rule, you’ll probably like the True Negation rule.  We see from the semantic rule for negations that if “~ ” is true…


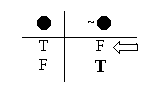
then “ ” must be false.



And now let’s say that again, using a vertical line.

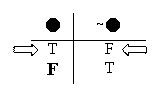
If “~ ” is true…


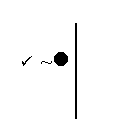
then “ ” must be false.


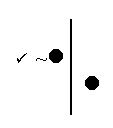
Between these two rules, we’ve rebuilt the semantic rule for negations, in our new format.


And we know that these rules together will cover any negation – because Bivalence tells us that every negation is either true, or else false.

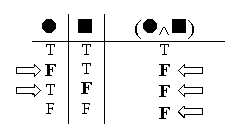
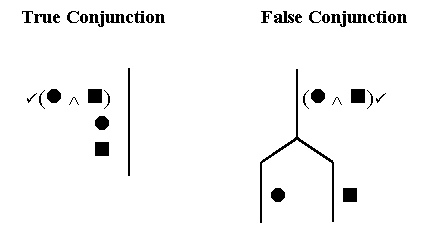
Next we retool the semantic rule for conjunctions; and once again, we read backward, from whole to parts.


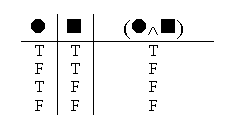
The first valuation tells us when the whole conjunction is true: the whole conjunction is true only when both of the parts are true.


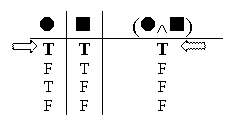
So – moving from the whole to the parts – if you find a conjunction which is true, you know both the parts must be true.


Next, we consider what happens if the whole conjunction is false.  This is more complicated, because (as Valuations 2 through 4 show us), there are three different ways to get a false conjunction.  If the whole conjunction is false, it might be because the left part is false (Valuation 2), or because the right part is false (Valuation 3), or because both parts are false (Valuation 4).


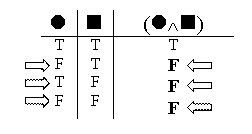
So how do we represent this, in vertical line notation?  We could just have the line split into three sub-lines, one for each of these valuations.  Then our rule for False Negations would look like this this


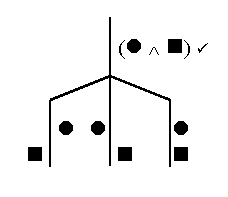
We could do that; but we’re not going to.  Why not?  Too much work!  We’re using the indirect test of validity to avoid work; and we’re using the vertical line notation to avoid work.  It’s all about avoiding work.  And since we’re trying to avoid work every chance we get, we’d rather only break the line into two lines, because two is less work than three.  For that matter, we’d really like to just stay with one line – because one line is less work than two.

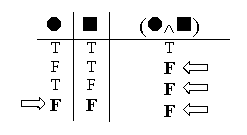
Well, we can’t get it all the way down to just one line – not if we want to state the Conjunction Rule accurately.  But we can get away with just two lines.  We can do that by eliminating the repetition in our original statement of the Conjunction Rule.  Look at it again:


We said there were three ways of making the whole conjunction false.  But in a sense, there are only two different ways of making the conjunction false: by having the left part false, or else by having the right part false.


We can state that as a rule: every time the whole conjunction is false, either the left part is false, or the right part is false.  What about Valuation 4, where both parts are false?  That’s nothing new – it’s just the overlap of the previous two case.  Valuation 4 is still a case where either the left or the right part is false – only here it’s both.


The rule for false conjunctions still holds: every time the whole conjunction is false, either the left part is false, or the right part is false (possibly both).


And now we state that rule in vertical line notation:


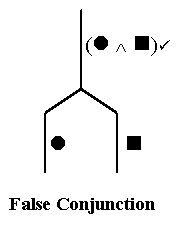
So we have the following two conjunction rules.


Finally, we rewrite the semantic rule for disjunctions.  In the case of disjunctions, the false case is the simple one: a disjunction is only false when both the part are false.


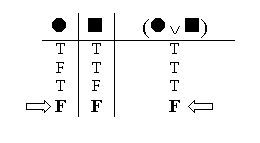
So we know that if the whole disjunction is false, both the parts are false.


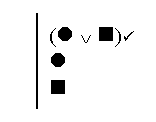
A true disjunction is more complicated, because there are three different ways to make the whole disjunction true: by having the left part true; by having the right part true; or by having both parts true.


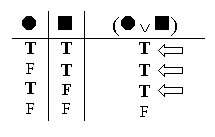
But using our experience with false conjunctions, we can distill these down to two core case: the situation where the right part is true, and the situation where the left part is true.


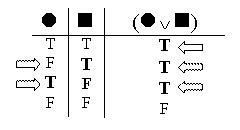
The third case, (Valuation 1), where both parts are true, is just the overlap of the other two cases.  So we can state the rule for true disjunctions: if the whole disjunction is true, then either the left part is true, or the right part is true.


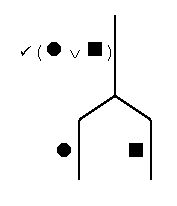
Now we’ve translated all our semantic rules, from the old T/F notation to the new vertical line notation.


We have all the ingredients we need for a completely streamlined semantic test of validity: (1) an indirect test (where we start out assuming that the argument is invalid); and (2) semantic rules in vertical line notation, to follow the consequences of that assumption all the way down to sentence letters.  The savings in labor will be incredible!