Circular Motion
Newton's Second Law
applied to a
Vertical Circle
What forces come into play as an aerobatic pilot does a barrel roll?
Or, for that matter, what forces come into play as you or I ride on one of today's roller coasters with hills and valleys and loops?
Please do not attempt to memorize -- and keep straight -- the force equations that we will derive for the different situations.
Rather, make a clear diagram and then apply Fnetac where ac is the centripetal acceleration so it -- and the net force or the centripetal force -- points toward the center of the circle. That's all there is!>
Always draw good, detailed "free body diagrams"! That is always important and it is especially important now. Never start by plugging numbers into equations and calculating an answer. Always start with a diagram!
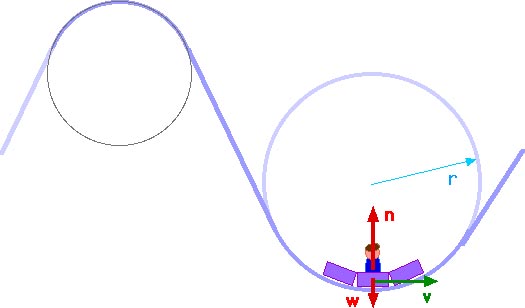
On top of a hill
The only forces acting on the rider are the upward normal force n exerted by the car and the downward force of gravity w, the rider's weight. These add together, as vectors, to provide the net force Fnet which is the centripetal force Fc, directed toward the center of the circle. The normal force may also be called the rider's "apparent weight" for this is the force of the seat on the rider and also describes what the rider "feels" (in addition to terror!).
Fnet = w - n = mg - n Fnet = Fc = m v2 / r
mg - n = m v2 / r
n = mg - m v2 / r
What does all this mean? The normal force or the rider's apparent weight is less than the rider's real weight. The seat can not exert a negative force on the rider. If we approach a situation where the apparent weight might become negative, there should be a good safety restraint system -- seat belts, lap bars, shoulder restraints, or something of that sort.
We might ask how fast the coaster can go until the rider just (barely) looses contact with the seat. That means the normal force between seat and rider is zero. That occurs for
n = mg - m v2 / r = 0 m v 2 / r = mg
v 2 / r = g
v 2 = g r
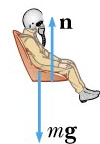
We have described this with a diagram showing a guest on the top of a hill of a roller coaster. The same ideas would apply, of course, to a pilot right-side-up on the top of a "roll" as shown here.
Bottom of a Valley
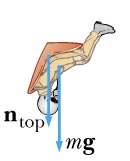
The only forces acting on the rider are the upward normal force n exerted by the car and the downward force of gravity w, the rider's weight. These add together, as vectors, to provide the net force Fnet which is the centripetal force Fc, directed toward the center of the circle. Notice, of course, that the center of the circle is now up from the rider. As always, the normal force may also be called the rider's "apparent weight" for this is the force of the seat on the rider and also describes what the rider "feels" (in addition to terror!).
Fnet = n - w = n - mg Fnet = Fc = m v2 / r
n - mg = m v2 / r
n = mg + m v2 / r
What does all this mean? The normal force or the rider's apparent weight is now more than the rider's real weight. The rider feels pressed down into the seat. And the feeling is more general. The rider's hands and arms are hard to move. The rider's blood is even hard to move. Airplane pilots are in this situation as they pull out of a dive. The ratio of this "apparent weight" to real weight may be described as the apparent effect of gravity or may be described as "g-forces". "g-forces" of six or seven -- meaning an apparent weight of six or seven times one's real weight -- can mean that enough blood will not be circulated to the brain and a pilot -- or other passenger -- may pass out.
Upside-down at the Top of a Loop
Now both the normal force n and the weight w point in the same direction so the net force is the sum of these two forces,
Fnet = n + w = n + mg Fnet = Fc = m v2 / r
n + mg = m v2 / r
n = ( m v2 / r ) - mg
What does all this mean? If the speed is too low, this equation says the normal force will be negative. What does a negative normal force mean? Since the seat can not reach out and pull you back, you will fall out of the car. And, since the track can not reach out and pull back on the roller coaster car, the car would fall off the track! To prevent this, roller coasters have wheels on both sides of the track! We might think of designing a ride so the normal force just vanishes and the victims do, indeed, feel weightless at the top. Or we might design a ride so the normal force is equal to the real weight at the top.
We have described this with a diagram showing a guest on the top of a loop of a roller coaster. The same ideas would apply, of course, to a pilot upside-down on the top of a roll as shown here.
Of course, there are other situations that provide vertical circles besides just a roller coaster. Aerobatic pilots or military pilots in dives and loops experience these same things. As you drive a hilly road you experience two of these three situations.
Table of Contents (c) Doug Davis, 2001; all rights reserved
