Vector Product

Consider two vectors, A and B,

 

We can define a new vector C,

C = A x B

The magnitude of C is

C = A B sin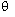

or

|C| = |A| |B| sin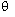

where is the angle between vectors A and B.

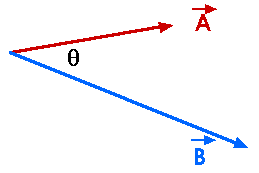
Remember, tho', that C is a vector. The direction of C is perpendicular to the plane define by vectors A and B. That is,

C A

and

C B

But that still leaves two possibilities for the direction of vector C. To find a single, unique direction, we shall employ (or invent) the right-hand rule.

The right hand rule: With the fingers of your right hand, rotate the first vector A into the second vector B. The direction your thumb points is the direction of the new vector C. (In this example, vectors A and B are in the plane of this page or screen and the new vector C points into the page or screen)

Vector products (also called "cross products") always involve three-dimensional visualizations. For our example here, if vectors A and B lie in the plane of the screen, then vector C is pointing into the screen.

Notice that this vector product is not commutative.

D = B x A

In fact, the cross product (or vector product) is anti-commutative; that is,

A x B = - B x A

With this basic definition of the vector product, what can we do with vectors A and B written in component or i, j, k notation?

A = A_x i + A_y j + A_z k

B = B_x i + B_y j + B_z k

 

| More on vector product. |

Rolling Motion			Torque
Return to ToC, Ch11, Rolling Motion

(c) Doug Davis, 2001; all rights reserved