Vector Product in ijk notation

Consider two vectors, A and B,

 

We can define a new vector C,

C = A x B C = A B sin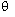

|C| = |A| |B| sin

Remember, tho', that C is a vector. The direction of C is perpendicular to the plane define by vectors A and B. With the fingers of your right hand, rotate the first vector A into the second vector B. The direction your thumb points is the direction of the new vector C. (In this example, vectors A and B are in the plane of this page or screen and the new vector C points into the page or screen)

With this basic definition of the vector product, what can we do with vectors A and B written in component or i, j, k notation?

A = A_x i + A_y j + A_z k

B = B_x i + B_y j + B_z k

C = A x B

C = [A_x i + A_y j + A_z k ] x [B_x i + B_y j + B_z k]

C = A_x B_x ( i x i ) + A_x B_y ( i x j ) + A_x B_z ( i x k ) +

+ A_y B_x ( j x i ) + A_y B_y ( j x j ) + A_y B_z ( j x k ) +

+ A_z B_x ( k x i ) + A_z B_x ( k x j ) + A_x B_x ( k x k )

What are these cross products of the unit vectors?

i x i = 0	i x j = k	i x k = - j
j x i = - k	j x j = 0	j x k = i
k x i = j	k x j = - i	k x k = 0

So our cross product becomes

C = A_x B_x ( 0 ) + A_x B_y ( k ) + A_x B_z ( - j ) +

+ A_y B_x ( - k ) + A_y B_y ( 0 ) + A_y B_z ( i ) +

+ A_z B_x ( j ) + A_z B_x ( - i ) + A_x B_x ( 0 )

C = i (A_y B_z - A_z B_y) + j (A_z B_x - A_x B_z ) + k (A_x B_y - A_y B_x)

That is certainly a good enough form to remember and we could stop here. But this expression can also be remembered as a determinant,

| Expanding determinants |

Vector Product (1)			Torque
Return to ToC, Ch11, Rolling Motion

(c) Doug Davis, 2001; all rights reserved